Portfolio Optimization. Application of the Markowitz Model Using Lagrange and Profitability Forecast

Keywordslagrangian modern portfolio theory stochastic process

JEL Classification C02, G11, G17

Full Article

1. Introduction

In this paper, the model elaborated by Harry Markowitz on the determination of the structure of the efficient securities portfolio is presented in a theoretical and applicative way. In this sense, to determine effective portfolio (PE) of Markowitz type is built and minimized a function of Lagrange type. Also, on the basis of the results obtained from the analysis, the profitability of the portfolio is modeled in continuous time and determines the range of values in which it can be found over one year after the analysis period. The data used in our analysis are shares of the financial investment companies (SIF), traded on the Romanian stock market on the Bucharest Stock Exchange (BVB).

One of the goals of this article is to make a comparison, by practitioners, of efficient portfolio structure, using the Markowitz model, with efficient portfolio structure, using the Sharpe model. This can be done by comparing the results obtained in this article with the results we have obtained in a previous article, titled: ”Portfolio optimization - application of Sharpe model using Lagrange” (Bratian, 2017).

In the following we make some clarifications on the importance of the studied subject. The founders of the modern theory of the portfolio are Harry Markowitz and his doctorate William Sharpe. In the view of the two researchers, the structure of the efficient portfolio (PE) is characterized by the minimum risk for a given level of expected profitability or equivalent, the maximum expected profitability for a given level of risk. This feature of the efficient portfolio is based on a criterion, the profitability-risk criteria, on the basis of which investors have a rational behavior aiming to obtain the lowest risk of the portfolio for a given level of expected profitability.

From a technical point of view, in portfolio theory, the expected profitability is given by the average, and the risk is given by the variance.”Markowitz postulated that an investitor should maximize expected portfolio return  while minimizing portfolio variance of return .” (Rubinstein 2002, p.1042).

The critique of the modern theory of the portfolio can be summed up precisely on the fact that the technique used is Gaussian, characterized by the two numerical sizes mentioned above. However, we must acknowledge that we do not have a well-structured alternative to this issue, and moreover, we must bear in mind that this theory has placed the field of finance on another level of knowledge. Robert Merton said, "Before the modern theory of the portfolio, finance was a collection of anecdotes, golden rules and manipulations of accounting information. The theory of the portfolio allowed the subsequent evolution from this mix to a rigorous economic theory." (Taleb, 2008, p. 315).

This being said, in addition to optimizing the portfolio, using the Markowitz model, we will determine, with different probabilities (0.99; 0.75), value ranges in which the return of efficient portfolio can be found at a time t in the future. In this sense, the return modeling will be carried out in continuous time.

We believe that this approach is especially useful for practitioners, because, in addition to determining the optimal portfolio structure, they can predict, with a certain probability, the range of values in which their return on investment will be at a time t in the future.

2. Literature Review

Markowitz (1952) proposes for the scientific debate the model in which investors, with varying degrees of aversion to risk, can determine the optimal structure of their portfolio of investments in financial assets. Sharpe (1963), realizes the diagonal model of portfolio optimization. Subsequently, modern portfolio theory takes a great deal the academic environment and for practitioners. Elton and Gruber (1997) and Rubinstein (2002), make some of the best synthesis of this theory's development over time. In Romania, the most recent empirical studies on this issue are conducted by Turcas et al. (2017); Zavera (2017).

Regarding the profitability forecast of the efficient portfolio (the second issue referred to in the paper), we find that the best known and most accepted model for assessing financial assets is the evaluation model in continuous time. (Wilmott, 2002, p. 75). As a result, the model we use to predict profitability is a stochastic model.

This being said, we are also making a very important statement that one of the works we consider to be relevant in terms of the importance and use of lagrangian in optimization problems is that of Fisher (2004).

3. Methodology

3.1. Concerning the Determination of the Efficient Portfolio Structure (PE) of Markowitz Type

The Markowitz Model for efficient portfolio structure (PE) provides investors the structure of the minimum risk portfolio for a given expected return greater than the expected return of the Minimum Risk Portfolio (PR_min).

In this optimization model, the objective function (minimizing portfolio risk, respectively minimizing portfolio variance value or minimizing portfolio volatility) has two restrictions, namely:

1.

2.

As a result, Lagrange (L) has the following formal expression (Dragota (coordinator) et al., 2009, p. 315):

(1)

To minimize L, the optimal conditions are:

(2)

The two above systems are equivalent because(Bratian (coordinator) et al., p. 355):

(3)

(4)

(5)

In matrix form, the last system above (2) is written as follows:

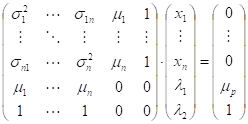(6)

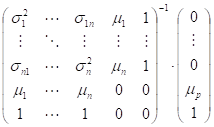= (7)

Variance and volatility (as measures of risk) of efficient portfolio return is determined as follows:

(8)

(9)

That being said, we recall that portfolios included between the minimum risk portfolio  and , are called efficient portfolios .

3.2. Concerning the Determination of the Structure of the Portfolio with Minimum Risk (Bratian, 2017, pp. 14-15)

Lagrange function for the minimum risk portfolio(PR_min)has the following formal expression (Dragota et al., pp. 282-283):

(10)

To minimize L, the optimal conditions are:

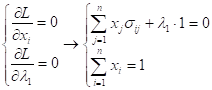(11)

The two systems above are equivalent because (Bratian (coordinator) et al., pp. 342-343):

(12)

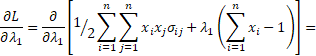
(13)

In the matrix expression, the above system (11) is written as follows:

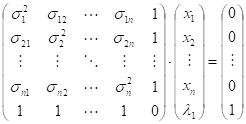(14)

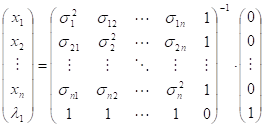(15)

The expected return () is given by the following formal expression:

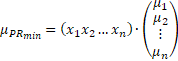(16)

Volatility of return for the minimum risk portfolio is determined as follows:

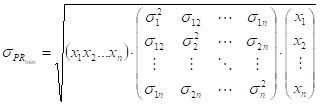(17)

3.3. Concerning the Profitability Forecast

Let be the following equation of motion of the value for the efficient portfolio of Markowitz type:

(18)

and either F = F(V) = lnV, the value for the efficient portfolio of Markowitz type.

Differential of F, using the Taylor series, is given by the following formal expression:

(19)

Knowing that:  and using heuristics , from (18) and (19), by substitution, we will have:

(20)

By integrating the expression (20), we obtain:

 , (21)

 where:

Next, given that at the initial moment the portfolio value is V(0), then the instant return for a certain period, until the moment t in the future is distributed as follows:

(22)

Because the instant return of the efficient portfolio of Markowitz type is normally distributed, it can be determined a confidence interval for this. Thus, with a probability of 99% or 75%, the portfolio's return at time t varies between the limits:

4. Application of theMarkowitzPortfolio Optimization Model to the Romanian Capital Market and Profitability Forecast

Next, we will apply the Markowitz portfolio optimization model and estimate the profitability of this portfolio over one year after the analysis period (252 days after 30.10.2017). In this respect, the methodology used is the one above, and the data used are the daily closing prices of shares of financial investment companies (SIFs) (BVB, 2018), which are logarithmated.

The analysis period is from 28.10.2016 to 31.10.2017 and is the same as the period used in a previous article (Bratian, 2017, pp. 8-21), where we analyze the Sharpe model. The choice of the same analysis period as in the previous article is, as we have said, also to be able to compare the structure of the Markowitz portfolio with the structure of the Sharpe portfolio.

Regarding the structure of the minimum risk portfolio (PR_min), the following values were obtained (Bratian, 2017, pp. 16-17):

- SIF1 shares = 21,46%;

- SIF2 shares = 7,61%;

- SIF3 shares = 42,41%;

- SIF4 shares = 7,78%;

- SIF5 shares = 20,74%.

For this portfolio structure, the expected return and the minimum risk are:

Observations: To the above expected return corresponds an expected return of 18.51% per year and to the above volatility corresponds an annual volatility of: 9.48%; prices and returns on portfolio securities are logarithmic.

Regarding the structure of the efficient portfolio (PE), using µ_PE = 0,09% (to this expected return corresponds an annual expected return of 22,68%), the following values were obtained:

*

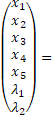
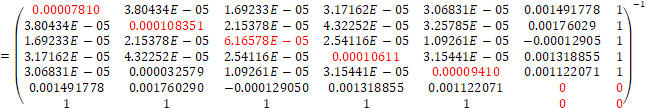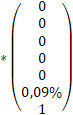
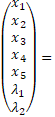
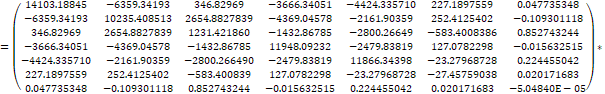
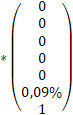
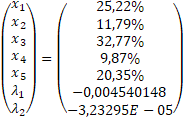
As a result of the calculations above, the structure of the efficient portfolio is:

- SIF1 shares = 25,22%;

- SIF2 shares = 11,79%;

- SIF3 shares = 32,77%;

- SIF4 shares = 9,87%;

- SIF5 shares = 20,35%.

For this structure, volatility is:

*

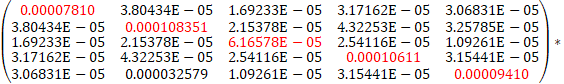
Remarks:

a) To the above volatility corresponds an yearly volatility of: 9,58%.

b) The calculations were made in Excel.

c) The prices and returns of the securities in the portfolio are logarithmic.

Regarding the profitability forecast for the efficient Markowitz portfolio, the following value ranges were obtained (with probability of 99% and 75% probability) and where t = 1 after one year:

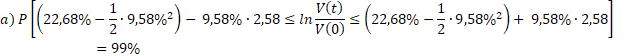
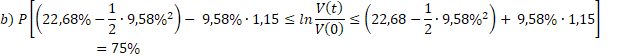
5. Conclusions

Following the Markowitz model, the structure of our efficient portfolio is as follows:

The expected return over one year after the analysis of the above-mentioned efficient portfolio is as follows:

a)

b)

References

1. Brătian, V., 2017. Portfolio optimization - application of Sharpe model using Lagrange. Revista Economică, 69(5), pp. 8-21.
2. Brătian, V., Bucur, A. and Opreana, C., 2016. Finanțe cantitative – evaluarea valorilor mobiliare și gestiunea portofoliului. Sibiu: Editura ULBS.
3. BVB, 2018. Bucharest Stock Exchange [online] Available at: www.bvb.ro  [Accessed on 12 March 2018].
4. Dragotă, V., Dragotă, M., Dămian, O., Stoian, A., Mitrică, E., Lăcătuș, C., Manațe, D., Țâțu, L. and Hândoreanu, C., 2009. Gestiunea portofoliului de valori mobiliare, ed. a 2-a. București: Editura Economică.
5. Elton, E. and Gruber, M. 1997. Modern portfolio theory, 1950 to Date. Journal of Banking & Finance, 21(11-12), pp. 1753-1759.
6. Fisher, M., 2004. The Lagrangian Relaxation Method for Solving Integer Programming Problems, Management Science, 50(12), pp. 1861-1871.
7. Markowitz, H., 1952. Portfolio Selection. The Journal of Finance, 7(1), pp. 77-91.
8. Rubinstein, M., 2002. Markowits’s „Portfolio Selection”: A Fifty –Year Retrospective. The Journal of Finance, LVII(3), pp. 1041-1045.
9. Sharpe, W., 1963. A Simplified Model for Portfolio Analysis. Management Science, 9(2), pp. 277-293.
10. Taleb, N., 2008. Lebăda Neagră – impactul foarte puțin probabilului. București: Editura Curtea Veche.
11. Turcas, F., Dumiter, F., Brezeanu, P., Farcaș, P. and Coroiu, S., 2017. Practical aspects of portfolio selection and optimisation on the capital market. Economic Research – Ekonomska Istraživanja, 30(1), pp. 14-30.
12. Wilmott, P., 2002. Derivative. Inginerie financiară – teorie & practică. București: Editura Economică.
13. Zavera, I., 2017. Application of Markowitz Model on Romanian Stock Market. Holistica, 8(1), pp.97-103.

Article Rights and License

Corresponding Author