Keywordsbook value forecast credit ratings earnings forecast equity valuation rating accuracy rating category performance distributions rating theory
JEL Classification G32, G12
Full Article
1. Introduction
Valuation is an integral part of finance, particularly in areas such as corporate finance, portfolio management and market efficiency studies(Damodaran,2007; Penman, 1998b). Prior studies have also examined the actions of credit rating agencies at both the corporate and sovereign bond level, and the effect that ratings have on various issuers, investors, pricing of company securities, financing strategies and monetary policies (Tusa,2016).
There is considerable literature on valuation models, with equity valuation typically presented as the forecasting of future payoffs discounted to present value. However, existing equity valuation (EV) models have shortcomings, and can be critiqued on a number of points. The accuracy of valuation models are generally affected by the assumptions (around key input variables) of the models (Nissimand Penman, 2001). One issue would be problems pertaining to forecasting over finite horizons, and the terminal value calculation (Steiger,2010). More importantly, EV models make a number of assumptions regarding the continual stability of equity and earnings (Damodaran,2007). For example, it is common to assume that earnings are not retained, and all earnings are paid out as dividends. Also, that assets and even earnings remain constant (Damodaran,2007).
In light of this, a valuation model that relaxes these assumptions regarding earnings and equity, is proposed. This is achieved by modelling earnings and equity as random processes via credit ratings and rating migration matrices.
A broad literature review discusses some of the salient papers on valuation, and offers an account of equity valuation models, ranging from the use of multiples and benchmarks in valuation, to discounted cash flow valuation, dividend discount models, residual income models and theoretical models. The literature review also looks at a brief history of the major credit rating agencies, and their influence on firms. A review of the existing literature suggests that it is possible to develop a more accurate equity valuation model through a better understanding of how credit ratings reflect on and inform EV.
The study works towards a more accurate valuation of equity, by focusing on a number of core premises:
1. Earnings to book value are comparable per rating category, and distinct across rating categories.
2. Firm asset growth is comparable per rating category, and distinct across rating categories.
3. The earnings of a company can be modelled as a random process, via earnings to book value probability distributions per rating category, and a rating migration matrix.
4. The equity of a company can be modelled as a random process, via growth probability distributions per rating category, and a rating migration matrix.
5. It is assumed that modelling earnings and equity as random processes would allow more accurate representations of the principal valuation inputs, and thus enable more accurate valuation.
Accordingly, the purpose of the study is to evaluate the premises of the proposed valuation model, in order to evaluate the practicality of the model. In particular, it addresses the following research propositions:
1. Earnings to book value are comparable per rating category, and distinct across rating categories.
2. Firm asset growth is comparable per rating category, and distinct across rating categories.
The study essentially examines the extent to which credit ratings inform equity valuation. Furthermore, the study mostly focuses on evaluating the premises of the proposed valuation model, and does not evaluate the accuracy of the proposed model itself. This is left to future research.
2. Literature Review
2.1. Credit Rating Agencies and Ratings
Credit ratings are produced by major credit ratings agencies (CRAs) (Gonzalezetal., 2004)namely: (a) Standard and Poor’s (S&P); (b) Moody’s and; (c) Fitch Group. Despite the existence of other smaller rating agencies, the credit rating market is dominated by S&P and Moody’s, which account for about 80% of all ratings (Kormos,2008; Rowland, 2005). CRAs provide quantitative and qualitative information beyond that which is publicly available, and provide a measure with respect to credit worthiness: an entity’s ability to service its debt and other financial obligations in time and in full, under varying conditions (CantorandPacker, 1996; Gonzalez et al., 2004; Reiter and Ziebart, 1991).
The major CRAs rate bonds according to their credit risk on a ratings scale from AAA (highest) to C (or a similar scale), which represents a rating from investment-grade to unsafe speculative-grade ratings, as shown in table 1 (DeHaanandAmtenbrink, 2011; Rowland, 2005). Because CRAs’ methods are not stated explicitly (ErdemandVarli, 2014), understanding ratings and their effect on firms and markets has long been a subject of interest. In a seminal paper by Cantor and Parker (1996), employing a regression analysis on pooled data of 35 countries, and based on OLS estimations, it was found that over 90% of the variability in determining S&Ps and Moody’s ratings can be explained primarily by 6 factors: per-capita income, strong Gross domestic product (GDP) growth, inflation rate, a country’s external debt, a country’s default history, and its level of economic development (CantorandPacker, 1996). The strong correlation between default risk and GDP growth, in addition to other macroeconomic factors, has been supported in other studies (ErdemandVarli, 2014; Rowland, 2005).
Table 1. S&P’s, Moody’s and Fitch rating scale
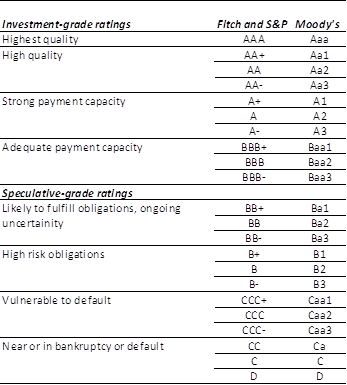
Source: De Haan and Amtenbrink, 2011
In 1975, the Securities and Exchange Commission (SEC) ruled that ratings should come from a national recognized statistical rating organization (NRSRO) after which the SEC then assigned NRSRO status to the big 3 CRAs, S&P, Moody’s and Fitch (Kormos,2008). Despite CRAs stating that ratings are only opinions (DeHaanandAmtenbrink, 2011), several regulations and laws backing NRSRO ratings as a standard, effectively institutionalized the influence and power of CRAs (Kormos,2008). Consequently, there is a growing reliance on CRA’s opinions. For instance, an analysis by Hill and Faff (2010) on a sample of 101 countries, provides evidence of strong market reaction to CRA ratings, particularly to those of S&P in both crisis and non-crisis periods (HillandFaff, 2010). CRAs now play an important role in providing information that informs corporate financing strategies, portfolio governance and monetary policies (Gonzalezetal., 2004; Kisgen, 2006). Lower ratings from CRAs are associated with higher government yields and higher costs of financing by governments (Rowland,2005). Thus, to ease access to capital markets for financing, governments seek CRA ratings (Rowland,2005). Issuers within the same country are also affected, as they rarely achieve ratings higher than that of their government (Rowland,2005).
Given the influence that CRAs have, one would expect them to be as accurate and objective as possible. However, the criticism leveled against them indicates some shortcomings. The dominant remuneration policy is based on an issuer-pays model in which the bond issuer solicits and pays the CRA for a rating (DeHaanandAmtenbrink, 2011; Tusa, 2016). This can lead to potential conflicts of interest and “ratings shopping”, where an issuer, unhappy with a particular rating, retries with another CRA (DeHaanandAmtenbrink, 2011; Tusa, 2016). For instance, due to the potential future savings on debt issuance costs, Mählmann (2009) proposes that a firm undergoes a structural self-selection model in deciding to obtain an “optional” Fitch rating which may be a better rating than that of a S&P and Moody’s rating (Mählmann,2009). The effect of this is a reduction in the average corporate bond credit spread (Mählmann,2009). Unsolicited ratings do occur, but are thought to be less accurate, due to their heavy reliance on publicly available data (Kormos,2008). Much of the criticisms towards CRAs was prompted by their failure to handle the Enron case, and the Global Financial Crisis (GFC). Evidence suggests that they did not investigate Enron in-depth, that they may have colluded with them, and failed to act decisively in downgrading Enron, despite evidence of suspicious dealings (Kormos,2008). Furthermore they have been implicated in the collapse of the US housing market, and the GFC that followed, due to their continued reassurance of investors, whilst failing to properly assess and quickly downgrade the complex financial products in the sub-prime mortgage market (DeHaanandAmtenbrink, 2011).
2.1.1. Rating Migration Matrices
Rating migration matrices, calculated by comparing ratings at the beginning and at the end of a period only, are issued by the major CRAs, and measure the probability of a rating upgrade or downgrade along the ratings scale within a specific time horizon (Gonzalezetal., 2004).
Altman (1989) was one of the first researchers to propose a method of constructing transition matrices, and measuring default risk. His research looked at changes from initial bond issuance over a ten-year horizon, relative to a survival population, thus taking an approach similar to that of calculating mortality rates in actuarial science (Altman,1989). He observed that in the first four years post-issuance, all B and CCC rated securities outperformed other rating categories, and thereafter BB rated bonds continued to outperform all other categories (Altman,1989). In a follow-up paper, he again looked at rating migrations over a ten-year horizon post-issuance, in addition to investigating a S&P’s and Moody’s static pool of issuers by up to ten-years after formation of the pool, regardless of bond age (Altman,1996).
Credit rating migration matrices have historically been assumed to follow Markovian behavior, but evidence of non-Markovian behavior has been mounting (Nickelletal., 2000). For instance, using an ordered probit model based on Moody’s data from 1970 to 1997, variation in transition probabilities was found to mostly depend on the business cycle (Nickelletal., 2000). The obligor’s industry and time since bond issuance were other factors shown to affect transition probabilities (Nickelletal., 2000). Rating migration differences between issuers by industry type and sector have also been observed (KadamandLenk, 2008).
The importance of the business cycle noted by Nickell et al. (2000), was independently supported in another study, which further showed the existence of 2 different, distinct economic regimes, under which ratings transition differ (Bangiaetal., 2002). In one systematic credit portfolio stress test , U.S. business cycles were first separated into an expansion and contraction phase, followed by modelling the effect of underlying macroeconomic factors on asset quality (Bangiaetal., 2002). The authors showed that default probabilities increased in the contraction phase (Bangiaetal., 2002). To account for changes in business cycles, a Mixture of Markov Chains (MMC) model has been shown to be efficient in predicting credit migration risk in long time horizons, compared to through the cycle models (Feietal.,2012). This approach allows changes in default risk as the business cycle evolves, and can thus be used to inform increases in capital buffers during the expansion phase, and to free capital for lending during a contraction phase (Feietal.,2012).
Lando and Skøderberg (2002) analyzed rating transitions of a 17 year S&P dataset, by contrasting an estimator based on a discrete-time cohort against one based on a continuous time method (LandoandSkødeberg, 2002). The authors found evidence of non-Markovian behavior in the form of rating drifts, in addition to strong non-Markovian behavior for downgrades. Their use of continuous-time data is compelling, in that it gives more efficient estimates on rare event transitions within a year of successive downgrades, despite a default not having occurred for any single firm in the sample (LandoandSkødeberg, 2002).
Frydman and Schuermann (2008) proposed a parsimonious model mixture of 2 Markov chains that exhibited non-Markovian behavior of rating migrations when the mixture model was estimated using historical S&P credit ratings from 1981 to 2002 (FrydmanandSchuermann, 2008). The non-Markovian behavior exhibited by their mixture model, implied that the distributions of a firm’s ratings were dependent on both its current rating and historical ratings, a finding that can have economic significance. Given this non-Markovian behavior, the authors find that 2 firms with identical initial credit ratings can be assigned different future distribution of ratings (FrydmanandSchuermann, 2008).
Rating migrations are of value, as they affect pricing of bonds, derivative pricing models, and some bank policies limit the proportion of below investment grade loans that the bank can hold (Gonzalezetal., 2004; Jarrow et al., 1997; Jarrow and Turnbull, 1995). In some cases ratings determine the eligibility of asset investments and valuation (Gonzalezetal., 2004; Jarrow et al., 1997; Jarrow and Turnbull, 1995).
2.2. Equity Valuation Models
Valuation in finance covers a wide spectrum of equity valuation models that differ in terms of what they forecast, and how they forecast it. They may be premised on dividends, cash flow, operating profit, etc. (Penman,1998b). These models are used for example in corporate finance, portfolio management, and market efficiency analysis(Damodaran,2007; Penman, 1998b). The following sections review the common valuation methods and their foundations. A fundamental question relevant to this study is how credit ratings shape equity valuation through equity valuation models.
2.2.1. Valuation using Multipliers and Benchmarks
As noted by Penman (1998a), the use of multipliers is a popular valuation technique that is simple and yields good approximations when these multiples are applied to either earnings or book value (Penman,1998a). The simplicity lies in the use of one value, a “bottom line” figure, which in itself is an aggregation of information from either the income statement or the balance sheet (Penman,1998a). These values are then standardised, for example the price paid per stock as a multiple of earnings generated by the asset, which yields a trailing P/E ratio of historical earnings, or a forward looking P/E ratio indicating expected earnings per share (Damodaran,2007). The P/E ratio (PER) can be expressed as (Fernandez,2001):
|
|
(1) |
The use of multiples can vary widely by sector, as noted by Fernandez (2001) in his revision of 14 popular multiples used by analysts at Morgan Stanley Dean Witter. Fernandez concluded that P/E ratio and EV/EBITDA multiples were the most used (Fernandez,2001). In valuations using multiples, it is common to use comparable firms in the same sector that have similar fundamental variables in terms of growth rates, risk and cash flows, whereby the implicit assumption is that comparable firms will be similarly priced (Damodaran,2007). The basic formula for relative multiples of a firm with respect to similar firms in the market (Fernandez,2001), can be expressed as:
|
|
(2) |
Alford (1992) argues that industry wide categorisations of firms are more effective, compared to categorisations using only fundamentals, whilst Cheng and McNamara (2000) and Bhojraj and Lee (2002) argue that a combination of the 2 categorisation methods yields more accurate valuations (as cited in Damodaran, 2007). However, there is still a prediction error due to the categorization of firms as similar, if the firm profiles vary widely. In addition, the prediction error is affected by the number of firms in each sector, with fewer firms increasing the error margin (Damodaran,2007).
Beatty et al. (1999) introduce a method whereby an analyst applies subjective judgement to explain the difference between a firm’s multiple and that of a computed average, with the company being considered as overvalued if the fundamentals cannot explain the difference, and vice versa (as cited in Damodaran, 2007). The greatest weakness of this subjective method is that it introduces the analyst’s bias. Another method involves modifying the multiplier by considering its companion variable (Damodaran,2007).
2.2.2. Dividend Discount Model
In the dividend discount model (DDM), the basis is that when stocks are bought, the cash flows are either in the form of dividends during the holding period, or an expected price, which in itself is determined by future dividends at the end of the holding period (Damodaran,2007). The rationale of the model is that the value of stock is the sum of all expected future dividends, adjusted for risk, and discounted back to present value (Rossetal., 2000). The value of stock given for an infinite time horizon can be formally expressed as:
|
|
(3) |
where t is a time period; ![]() is the market price in that period;
is the market price in that period; ![]() is one plus the cost of equity;
is one plus the cost of equity; ![]() are future net dividends paid at each period
are future net dividends paid at each period ![]() ;
; ![]() is market expectation at time period
is market expectation at time period ![]() (Courteau et al., 2001). However, in practice analysts forecast over finite time periods, and thus this requires a terminal value or continuing value to be calculated, to correct for the truncation of the forecast horizon (Penman, 1998b, 2001).When the horizon is finite for time period
(Courteau et al., 2001). However, in practice analysts forecast over finite time periods, and thus this requires a terminal value or continuing value to be calculated, to correct for the truncation of the forecast horizon (Penman, 1998b, 2001).When the horizon is finite for time period ![]() , the intrinsic value
, the intrinsic value ![]() of the DDM is given by:
of the DDM is given by:
|
|
(4) |
At the end of the forecast period ![]() ,
, ![]() is the forecast stock price and
is the forecast stock price and ![]() is the “ideal” terminal value (Courteau et al., 2001).
is the “ideal” terminal value (Courteau et al., 2001).
Penman and Sougiannis (1998) take note of the Modigliani-Miller theorem, which in its simplest form states that the price of a firm is independent of the way it finances its investments, or of its dividends policy, and thus for going concerns, valuation over finite periods is uninformative about price (Penmanand Sougiannis, 1998). Some researchers have criticised the DDM as being too narrowly focused on dividends. However, the model has an advantage in that it relies on less assumptions to calculate forecasted dividends (Damodaran, 2007). If a dividend was paid in the preceding year, an estimated growth rate can be applied, assuming a perpetual stream of dividends which can then be discounted to present value (Damodaran, 2007). The DDM assumes that earnings are not retained. However, some companies hold back dividends, building cash reserves, resulting in the free cash flow to equity exceeding the dividends, and thus the DDM undervalues such companies, as the model does not make equity claims on built up cash balances (Damodaran, 2007). Alternatively, a company can pay out far more dividends than it has cash flows, and the DDM in this case would over value the company, as the model assumes that this level of dividends will be sustained in perpetuity, as it is assumed that the company can continue to draw on external funding to pay those dividends (Damodaran, 2007).
2.2.3. Discounted Cash Flow Valuation
The discounted cash flow valuation (DCF) method is a popular, standard method of not only valuing companies, but in pricing initial public offerings (Steiger,2010). Penman (1998) states that expected earnings are equal to:
|
|
(5) |
Where ![]() is the free cash flow from operating assets, and
is the free cash flow from operating assets, and ![]() is the interest gained from financial assets (Courteau et al., 2001; Penman, 1998b).
is the interest gained from financial assets (Courteau et al., 2001; Penman, 1998b).
It has long been recognized that the clean surplus relation (CSR) holds for net financial assets (FA) for all t > 0 (Courteauet al., 2001):
|
|
(6) |
Rewritten, the equation can be expressed as:
|
|
(7) |
Equation 6 bears similarity to the DDM. ![]() from equation 3 can be substituted with equation 7. For an infinite horizon, Penman (1998b) derives the following DCF model as shown in equation 8 (Penman,1998b):
from equation 3 can be substituted with equation 7. For an infinite horizon, Penman (1998b) derives the following DCF model as shown in equation 8 (Penman,1998b):
|
|
(8) |
Feltham and Ohlson (1995) state that equation 8 represents cash accounting where operating assets are expensed; book value is represented by current net financial assets; and “earnings” are represented by free cash flows from operations, ![]() , plus (minus) interest income (expense),
, plus (minus) interest income (expense), ![]() (as cited in Courteau et al., 2001). If the assumption of risk neutrality is relaxed, but net financial assets are assumed to always be marked to market, the equation becomes the free cash flow model (Penman,1998b):
(as cited in Courteau et al., 2001). If the assumption of risk neutrality is relaxed, but net financial assets are assumed to always be marked to market, the equation becomes the free cash flow model (Penman,1998b):
|
|
(9) |
There are up to 10 variations of valuation using discounted cash flows, and in his analysis of these methods, Fernandez (2007) showed that the same value was calculated by each method when applied to a similar example, and that the only difference between methods was that of the cash flows taken at the starting point of valuation (Fernandez, 2007).
2.2.4. Residual Income Model (RIM)
In cases where a company does not pay dividends, the residual income model (RIM) can be used, which utilizes the excess between actual and realized earnings of a firm, or residual income (Rossetal., 2000). It has been established theoretically that the DCF is equivalent to the RIM under finite time horizons (Courteau et al., 2001). The “ideal” terminal value for the RIM has been shown by Penman (1997) to be the market’s expected premium at the end of a finite horizon T, expressed as ![]() (as cited in Courteau et al., 2001). The terminal value reflects the present value of abnormal earnings,
(as cited in Courteau et al., 2001). The terminal value reflects the present value of abnormal earnings, ![]() , for the forecast year, and the RIM employing a terminal value is expressed as:
, for the forecast year, and the RIM employing a terminal value is expressed as:
|
|
(10) |
Without a terminal value, and assuming simple perpetuity and constant growth, alternate equations are (Courteau et al., 2001):
|
|
(11) |
|
|
(12) |
2.2.4.1. Other Models
Zhang (2000) introduces a real-options-based model that combines a valuation model by Ohlson (1995) with that of Feltham and Ohlson (1995; 1996). Capital investment decisions capture the nonlinearity of accounting variables in relation to equity value (Zhang, 2000). A simplified version of the Zhang (2000) model (Chen and Zhang, 2007) can be expressed as:
|
|
(13) |
At the end of period t, ![]() is the value of a firm financed by equity alone,
is the value of a firm financed by equity alone, ![]() is the book value,
is the book value, ![]() are the growth opportunities,
are the growth opportunities, ![]() are the earnings generated, and
are the earnings generated, and ![]() is the expected earnings generated from assets. The capitalisation factor that converts expected returns into a value metric, is represented by k.
is the expected earnings generated from assets. The capitalisation factor that converts expected returns into a value metric, is represented by k.
The model specifies a firm in a multi-variable setting, in which it either expands when profitable, or discontinues operations when it is not profitable, as represented by the call option, ![]() , and put option,
, and put option, ![]() , respectively in equation 13 (Chen and Zhang, 2007). Equation 13 states that the equity value of a firm is dependent on the value generated from existing operations, plus value from growth opportunities and abandonment options (Chen and Zhang, 2007). To simplify the analysis, Zhang (2000) assumes that a firm’s profitability, (
, respectively in equation 13 (Chen and Zhang, 2007). Equation 13 states that the equity value of a firm is dependent on the value generated from existing operations, plus value from growth opportunities and abandonment options (Chen and Zhang, 2007). To simplify the analysis, Zhang (2000) assumes that a firm’s profitability, (![]() ), follows a random walk (Zhang, 2000):
), follows a random walk (Zhang, 2000):
|
|
(14) |
|
|
(15) |
The valuation function in equation 15 now gives the equity value as a product of the amount of equity invested, ![]() , and the value per unit of capital
, and the value per unit of capital ![]() , which is a function of
, which is a function of![]() : profitability, growth opportunities, and the discount rate respectively (Chen and Zhang, 2007). As stated previously, the model specifies the firm in a variable setting, with the ability to downscale or upscale operations depending on profitability, and it is this flexibility that makes
: profitability, growth opportunities, and the discount rate respectively (Chen and Zhang, 2007). As stated previously, the model specifies the firm in a variable setting, with the ability to downscale or upscale operations depending on profitability, and it is this flexibility that makes ![]() a convex function of
a convex function of ![]() (Chen and Zhang, 2007; Zhang, 2000).
(Chen and Zhang, 2007; Zhang, 2000).
2.2.5. Concluding Remarks on Existing Valuation Models
In general, a review of current research indicates that equity valuation techniques have not progressed much, as the main focus has been on models derived from either the DDM, DCF, or RIM model (Nissim and Penman, 2001). Some researchers, like Zhang (2000), have sought to improve upon the existing valuation models, with new theoretical models (Zhang, 2000). Penman (1998) argues that models that forecast dividends, are related to one another over finite time horizons, and that the determining factor is the terminal value calculation, and not the attributes to be forecasted (Penman, 1998b). Given problems with the ad hoc nature of calculating the “ideal” terminal value, and other shortcomings of existing valuation models, an ability to accurately forecast over finite time horizons, also in a more informative way, is the main motivation in researching alternative equity valuation models, also given that forecasting dividends in the short term is not a true indication of the value of expected dividends in the long run (Penman, 2001).
3. An Equity Valuation Model based on a Random Process Modelling of Earnings and Growth
Existing equity valuation models are rendered inaccurate by various underlying assumptions, that include the expected levels of growth rates in earnings, whether or not the growth rate is in perpetuity, payout ratios, and ad hoc terminal value calculations. To improve valuation accuracy, a model is proposed and considered that commences from the DDM, and prices equity according to dividends, when modelling earnings and growth through random processes. A DDM equivalent model over an infinite horizon can be expressed as equation 16, and as equation 17 over a finite period:
|
|
(16) |
|
|
(17) |
Where ![]() is the forecast time horizon;
is the forecast time horizon; ![]() and
and ![]() are the market price at time
are the market price at time ![]() and
and ![]() respectively; and
respectively; and ![]() is the future dividend paid at time
is the future dividend paid at time ![]() . As shown below, the dividend is modelled based on earnings, and earnings itself is modelled as a random process. A notable feature of this model is that the distribution of dividends is assumed to be a random process, and thus a risk free rate is applied at time
. As shown below, the dividend is modelled based on earnings, and earnings itself is modelled as a random process. A notable feature of this model is that the distribution of dividends is assumed to be a random process, and thus a risk free rate is applied at time ![]() , denoted by
, denoted by ![]() , instead of a required rate of return on equity. In this context, the required rate of return on equity would relate to the earnings random process and distribution.
, instead of a required rate of return on equity. In this context, the required rate of return on equity would relate to the earnings random process and distribution.
As noted in section 2.2.2, the DDM assumes a scenario where no earnings are retained, but in practice some companies hold back dividends, and in some scenarios pay out dividends greater than cash flows. If the assumption is relaxed that earnings are not retained, then, to cater for the different dividend scenarios, a variable heuristic ![]() can be applied to earnings
can be applied to earnings ![]() , to determine future dividends
, to determine future dividends ![]() paid at time
paid at time ![]() . This is depicted by equation 18:
. This is depicted by equation 18:
|
|
(18) |
![]() in equations 16 and 17 can thus be substituted by equation 18. In simplest form, the heuristic can be expressed as a percentage of earnings, and if earnings are not retained, the dividend calculation reverts back to that of the DDM. Alternatively, the heuristic can be a variable rate, dependent on the profitability and growth of the firm. The assumption is that healthier firms are more likely to pay out dividends, compared to less healthy firms. Also, firms may retain earnings while they are experiencing growth.
in equations 16 and 17 can thus be substituted by equation 18. In simplest form, the heuristic can be expressed as a percentage of earnings, and if earnings are not retained, the dividend calculation reverts back to that of the DDM. Alternatively, the heuristic can be a variable rate, dependent on the profitability and growth of the firm. The assumption is that healthier firms are more likely to pay out dividends, compared to less healthy firms. Also, firms may retain earnings while they are experiencing growth.
Earnings is modelled as a Markov process, ![]() , and related to a firm’s probability of migrating across rating categories, according to a credit rating migration matrix. This is expressed in equation 19. The premise and assumption are that firms within the same rating category have similar probability distributions of earnings to book value ratios. Also, rather than modelling earnings directly, earnings to book value is modelled instead. The objective is to standardize earnings, so that it can be compared across companies and across credit ratings. Earnings may not be comparable across comparable firms, but earnings to book value may very well be. Firm specific factors such as company size can affect earnings. Therefore, to determine earnings independently of these factors, earnings to book value is utilized. Earnings is derived from the book value of the preceding interval,
, and related to a firm’s probability of migrating across rating categories, according to a credit rating migration matrix. This is expressed in equation 19. The premise and assumption are that firms within the same rating category have similar probability distributions of earnings to book value ratios. Also, rather than modelling earnings directly, earnings to book value is modelled instead. The objective is to standardize earnings, so that it can be compared across companies and across credit ratings. Earnings may not be comparable across comparable firms, but earnings to book value may very well be. Firm specific factors such as company size can affect earnings. Therefore, to determine earnings independently of these factors, earnings to book value is utilized. Earnings is derived from the book value of the preceding interval, ![]() , and the earnings to book value ratio of the preceding interval,
, and the earnings to book value ratio of the preceding interval, ![]() , as shown in equation 19. This standardizes the earnings of different firms, and is ideal in that it allows clustering, segmentation and ranking, specifically of earnings, and particularly in the context of credit rating categories, as well as equity valuation. Thus, current earnings can be expressed as:
, as shown in equation 19. This standardizes the earnings of different firms, and is ideal in that it allows clustering, segmentation and ranking, specifically of earnings, and particularly in the context of credit rating categories, as well as equity valuation. Thus, current earnings can be expressed as:
|
|
(19) |
|
|
(20) |
In equation 20, ![]() is the probability of firm
is the probability of firm ![]() having rating
having rating ![]() in interval
in interval ![]() ;
; ![]() is the probability of migrating from rating category
is the probability of migrating from rating category ![]() to
to ![]() ;
; ![]() is the number of rating categories;
is the number of rating categories; ![]() is the current rating category of interval
is the current rating category of interval ![]() ;
; ![]() is the earnings to book value probability distribution of rating category
is the earnings to book value probability distribution of rating category ![]() .
. ![]() is the book value of firm
is the book value of firm ![]() at interval or time
at interval or time ![]() .
. ![]() is the book value of firm
is the book value of firm ![]() at interval
at interval ![]() .
. ![]() relates to, and is related to, the book value growth distribution of rating category
relates to, and is related to, the book value growth distribution of rating category ![]() :
: ![]() considers and progresses the initial book value of the firm, by considering the book value growth distributions of rating categories, and the rating migration of the firm – the rating categories the firm migrates to.
considers and progresses the initial book value of the firm, by considering the book value growth distributions of rating categories, and the rating migration of the firm – the rating categories the firm migrates to.
Thus, the book value of the firm is equally modelled as a random process. A Markov process is used to progress the book value of the firm, by relating it to the rating category progression of the firm, via a rating migration matrix, and by relating it to the book value growth distributions of rating categories. Again, the premise and assumption are that firms within the same rating category have similar probability distributions of book value growth.
|
|
(21) |
|
|
(22) |
It should be noted that, in the above, (method to calculate) firm earnings and book value probability distributions are really proposed.
3.1.Research Objectives
In light of the proposed equity valuation model, the purpose of the study is to examine some of the fundamental premises of the proposed model. In particular, the study seeks to investigate and establish the following research propositions:
1. Earnings to book value are comparable per rating category, and distinct across rating categories.
2. Firm asset growth is comparable per rating category, and distinct across rating categories.
4. Methodology
In general, the research population comprises all publicly-traded equity in a particular market, that are rated by a rating agency. The research sample comprises all publicly-traded, and credit rated equity, listed on the JSE and NYSE stock exchanges. The sample was limited to all equity of the major rating categories (AAA, AA, A, BBB, BB, B), rated by at least one major CRA, and for the window period 2009 to 2017.
A portfolio of listed companies with ratings, was obtained from Bloomberg Professional service terminals. Company earnings per share, book value per share, and shares outstanding data was collected. Company historical ratings data was extracted from ratings changes data.
Companies for which the earnings per share, book value per share, and shares outstanding data was incomplete over the window period 2009 to 2017, were excluded. The JSE dataset comprised 60 unique companies, and 322 observations, whilst the NYSE dataset had 999 unique companies, and a total of 3687 observations.
Earnings were calculated by multiplying the earnings per share by the shares outstanding, whilst a product of the book value per share and shares outstanding gave the book value. The earnings per book value of the data set was then calculated by dividing the calculated earnings by the calculated book value. Credit rating data was used to group similarly rated companies by their major rating categories (AAA, AA, A, BBB, BB, B). In addition, differentials (deltas) per company earnings and growth processes across intervals, were calculated and used to calculate the probability distributions per rating category.
Data analysis was done in RStudio version 1.1453, running version 3.5.1 of R (RCoreTeam, 2018). In addition to the core functions available in R, the following free packages, distributed under version 3 of the GNU Affero General public license, were used to aid in analysis and presentation of results: ggplot2, scales, ggthemes, sqldf, car, readr, desc and ppcc.
Utilizing R, the characteristics and distinctness of the distributions of earnings and book value were examined, and cross-compared across rating categories – the general nature and shape of the distributions, as well as whether distributions are distinct across rating categories. Descriptive statistics performed in R, provided summaries of the dataset, on which a number of inferences were based. Where applicable, the uniqueness of distributions across rating categories were statistically tested. Also where applicable, the distributions were tested for normality, as a form of testing distinctness. This was accomplished by parsing the collected data as a vector into R, and constructing probability plots in the form of quantile quantile (QQ) plots, to compare the distributions and to measure the correlation to a theoretical normal distribution.
5. Results
5.1.Earnings per Book Value
The cumulative frequency distributions shown in figures 1-12 represent the 8 year (2009-17) earnings per book value distributions of listed companies across rating categories AAA through to B. Figures 1-7 show this relationship for JSE listed companies, whilst Figures 8-12 pertain to the sample of NYSE listed companies. In figures 1-7 and figurers 8-12, plots with red markers represent all data available for that rating category, whilst plots with black markers represent the same relationship, after outliers have been excluded. Table 2 and table 3 provide summary statistics, by rating category, for earnings per book value, before and after excluding outlier data, for both the JSE and NYSE markets respectively.
In the first set of results of cumulative frequency distributions, extreme values not fitting the overall pattern were misrepresenting the data, as is evident from the red plots. Once extreme values were excluded, the cumulative frequency distributions and corresponding QQ plots could be better interpreted, and inferences became easier to make. Cross-market comparisons between the JSE and NYSE market were made possible by the use of standardised earnings per book value, resulting in a standardised measure independent of company-specific factors.
After excluding outliers, figure 7 shows a comparison of the earnings per book value of JSE listed companies for rating categories AAA to rating category B. A comparison of the earnings per book value of NYSE listed companies for rating categories AA to B is illustrated in figure 13. Figure 14 and figure 15 report results across the 2 markets, and compare the 8 year (2009-17) earnings per book value of listed companies of the JSE and NYSE markets, respectively, after excluding outlier earnings data. Table 4 and table 6 show the results of Levene’s test performed on the JSE and NYSE data respectively, to test whether variance in earnings per book value were equal across rating categories. The results of a two-sample T-test that tests for equal means of earnings per book value across rating categories, are shown in table 5 and table 7, for the JSE and NYSE data respectively.
5.1.1. Inferences from the Descriptive Statistics
As shown in table 2, for the JSE data set, there was a gradual decrease in the minimum and 1st quartile values of earnings per book value across rating categories, except for rating category BBB. An increase was observed for the maximum, median and 3rd quartile values of earnings per book value, but there is a loss of consistency in these measures across rating categories BBB, BB and B. The mean of earnings per book value gradually decreased consistently across rating categories, except for rating category B. The mean of earnings per book value in the case of rating category B may have been influenced by companies with high earnings per book values. Standard deviation is a measure of data dispersion from the mean, and there was a trend towards an increase in standard deviation of earnings per book value, and thus variability in earnings per book value, across rating categories, except for rating categories BBB and B.
With regards to the NYSE data set, and as shown in table 3, the minimum and mean of earnings per book value gradually decreased from rating category AA to B, except for rating category BB. Starting at AA, the 1st and 3rd quartiles, as well as the median values, of earnings per book value show a consistent pattern of a gradual decrease across rating categories. The maximum of earnings per book value show a gradual increase across rating categories, except for rating category BBB. The interquartile range, which covers the range of the middle 50% of the observed earnings per book value, shows a consistent and gradual increase in values across rating categories. The standard deviation of earnings per book value increases across rating categories, except for rating category BBB, and points to variability in earnings per book value between rating categories.
5.1.2. Statistical Testing of Distinctiveness of Earnings per Book Value across Rating Categories
Levene’s test is an inferential statistic that was used in this study to test the null hypothesis that the variance of earnings per book value across rating categories are equal. For the tests, a significance cut-off of 0.05 was used. Overall, the P values for the JSE and the NYSE earnings per book value were found to be significant, as shown in table 4 and table 6 respectively. This then implies that the overall variances of earnings per book value across rating categories are not equal, and that the null hypothesis can therefore be rejected.
For the JSE data, the same conclusion is generally reached. P values across rating categories are significant, except across rating category BB and B, which had a P value of 0.1469. For the NYSE data, the P values across rating categories were found to be significant, except across rating categories A and BBB.
A two-sample T-test was then performed to test the null hypothesis that the mean values of earnings per book value across 2 rating categories are equal. The alternative hypothesis is then that the mean values of earnings per book value across 2 rating categories are not equal. The T-test assumes that the groups are random, sampled from normal distributions, and independent. In addition, the T-test assumes equal variance. Based on Levene’s test, this is an appropriate statistical test, only across rating categories BB and B, for the JSE data. Similarly, the T-test could only be used across rating categories A and BBB, for the NYSE data, where Levene’s test was not significant. Welch’s T-test was therefore used as an appropriate statistical test across all other rating categories. This is an adaptation of the T-test, that modifies the number of degrees of freedom to cater for unequal sample sizes and unequal variances, as confirmed by Levene’s test. In all cases, a significance cut-off of 0.05 was used.
For the JSE data, the P value of Welch’s T-test was found to be significant only across rating categories BBB and BB. The T-test performed across rating categories BB and B was found to not be significant. For the NYSE data, Welch’s T-test was significant only across rating categories BB and B, whilst the T-test was significant across ratings A and BBB.
Based on these results, the null hypothesis that the means across rating categories are equal, is rejected, but only across rating categories BBB and BB for the JSE data, and only across rating categories A and BBB, and across rating categories BB and B, for the NYSE data.
5.1.3. Normality of Distributions
Quantile-quantile (QQ) plots were used to compare the earnings per book value distributions of rating categories, to that of quantiles from a theoretical normal distribution. For both markets, earnings per book value data that excludes outliers, was used. Figures 16 to figure 21 (JSE data), and figures 22 to 26 (NYSE data) delineate the QQ plots per rating category.
The statistical package used, R, draws a straight line which passes through the first and third quantiles. If taken from a normal distribution, the sample data is expected to fall along this straight line. To make inferences from the data, the correlation or degree of fit was also quantified.
For the JSE dataset, it is difficult to make inferences from the data of rating category AAA, due to the reduced sample size, which results in variability. Despite the small sample size, the correlation coefficient, and the shape of the QQ plot implies a normal distribution. As the sample size increases across the rating categories, this distribution becomes more apparent, but with heavier tails than expected from a normal distribution. The heavy tails are shown by the deviation from the straight line, at either the left or right tail ends of the QQ plots, indicating data values smaller or greater than expected, respectively. This is in line with the observed general pattern of a decrease in the minimum earnings per book value, and an increase in maximum values, across rating categories.
For the NYSE market, the QQ plots can be seen to follow the same trend as the JSE data, for rating categories AA to B that can be cross-compared. Rating category AA has the least number of observations in the NYSE data set, and as such the distribution is not as evident in the QQ plot. Similar to the JSE data, as the sample size increases, the QQ plots show that the distribution more closely approximates a normal distribution. The NYSE data however has slightly lower correlation coefficients, compared to the SA QQ plots, a by-product of the heavier tailed distributions, in particular for rating categories A through to B. Overall, the NYSE data displays much heavier tailed distributions than the SA data, more so than would be expected for a normal distribution. Nevertheless, for both datasets, there is a trend towards more data spread for the more speculative rating categories, relative to the investment grade ratings.
5.1.4. Conclusion
In general, the observed patterns within the data across rating categories, highlight results that are consistent with the first proposition. As expected, firms with the same rating category, have similar distributions of earnings per book value. Also, there is generally a consistent relationship and progression in and of earnings per book value across rating categories. There is sufficient differentiation in the earnings per book value of firms across rating categories, as shown in figure 13. This finding of a distinct relationship between earnings distributions and ratings applies more strongly to the NYSE data, and the differentiation between rating categories is less obvious for the JSE data, as shown in figure 7, due to the smaller sample size.
The small number of observations in the JSE data set hampered fully reliable analysis. Nevertheless, it can be said that the trend in the JSE data set is approximating that of the NYSE data set, which had a larger sample size. Compared to the JSE data, the NYSE data shows earnings per book value with a general pattern of data spread that is less tightly clustered around the median, with a move towards the more speculative rating categories.
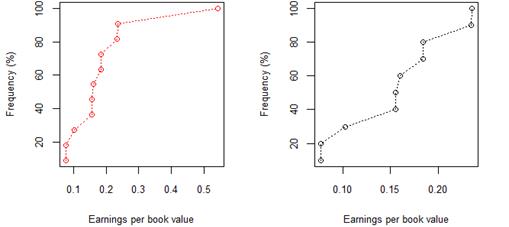
Figure 1. South African 8 year (2009-17) earnings per book value for rating category AAA before and after excluding companies identified as outliers
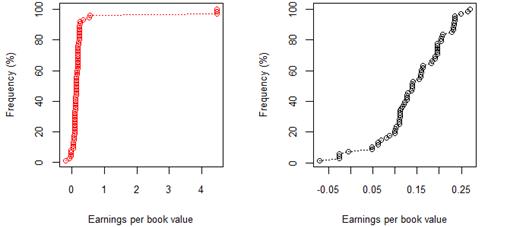
Figure 2. South African 8 year (2009-17) earnings per book value for rating category AA before and after excluding companies identified as outliers
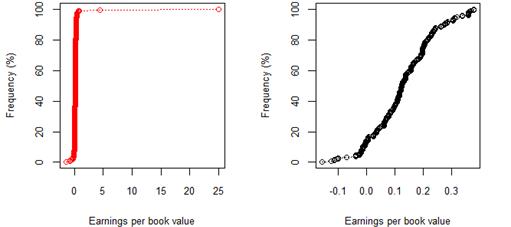
Figure 3. South African 8 year (2009-17) earnings per book value for rating category A before and after excluding companies identified as outliers
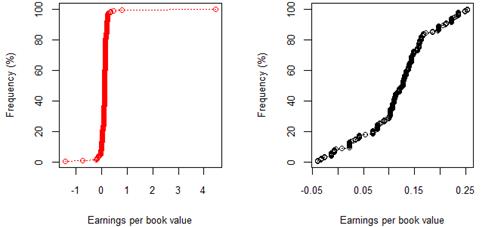
Figure 4. South African 8 year (2009-17) earnings per book value for rating category BBB before and after excluding companies identified as outliers
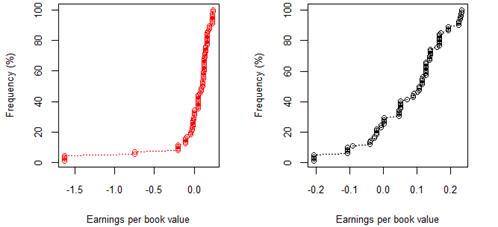
Figure 5. South African 8 year (2009-17) earnings per book value for rating category BB before and after excluding companies identified as outliers
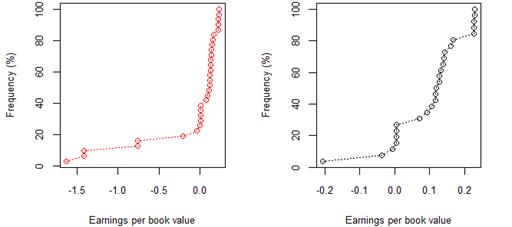
Figure 6. South African 8 year (2009-17) earnings per book value for rating category B before and after excluding companies identified as outliers
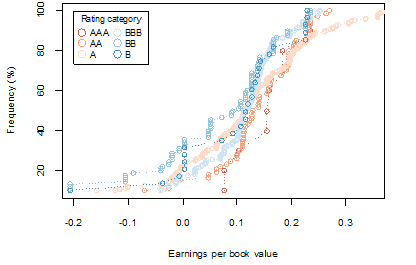
Figure 7. A comparison of JSE 8 year (2009-17) earnings per book value by rating categories AAA to B after excluding companies identified as outliers
Table 2. Summary statistics of JSE earnings per book value by rating category
| JSE data | AAA | AA | A | BBB | BB | B | ||||||
| All data | After exclusions | All data | After exclusions | All data | After exclusions | All data | After exclusions | All data | After exclusions | All data | After exclusions | |
| No. of observations | 11 | 10 | 75 | 68 | 259 | 241 | 212 | 198 | 88 | 82 | 31 | 26 |
| Min | 0.0768 | 0.0768 | -0.1735 | -0.0708 | -1.4108 | -0.1585 | -1.4108 | -0.0396 | -1.6249 | -0.2071 | -1.6249 | -0.2071 |
| 1st Quartile | 0.1288 | 0.1157 | 0.1103 | 0.1103 | 0.0577 | 0.0618 | 0.0768 | 0.08215 | -0.0199 | 0.0036 | -0.0015 | 0.02053 |
| Median | 0.1598 | 0.157 | 0.1553 | 0.14 | 0.1247 | 0.1247 | 0.1247 | 0.1271 | 0.10425 | 0.11135 | 0.1162 | 12355 |
| Mean | 0.1916 | 0.1565 | 0.324 | 0.1423 | 0.2352 | 0.1295 | 0.1252 | 0.11754 | -0.01873 | 0.07731 | -0.1067 | 0.10214 |
| 3rd Quartile | 0.2094 | 0.1842 | 0.2052 | 0.1957 | 0.2036 | 0.1981 | 0.1576 | 0.15702 | 0.1412 | 0.15507 | 0.1416 | 0.15563 |
| Interquartile range | 0.0806 | 0.0685 | 0.0949 | 0.0854 | 0.1459 | 0.1363 | 0.0808 | 0.07487 | 0.1611 | 0.15147 | 0.1431 | 0.1351 |
| Max | 0.5426 | 0.2353 | 4.4504 | 0.27 | 24.9793 | 0.3782 | 4.4504 | 0.2528 | 0.2345 | 0.2345 | 0.229 | 0.229 |
| Standard deviation | 0.1285 | 0.0572 | 0.8545 | 0.0736 | 1.5781 | 0.1081 | 0.3367 | 0.0670 | 0.3886 | 0.1115 | 0.5148 | 0.1019 |
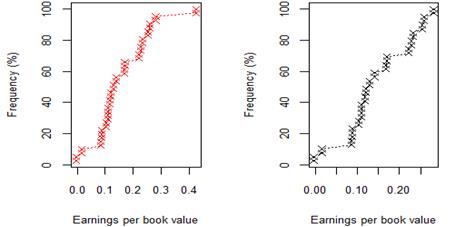
Figure 8. New York 8 year (2009-17) earnings per book value for rating category AA before and after excluding companies identified as outliers
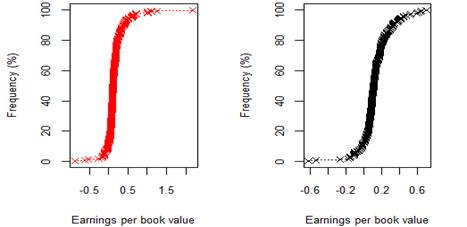
Figure 9. New York 8 year (2009-17) earnings per book value for rating category A before and after excluding companies identified as outliers
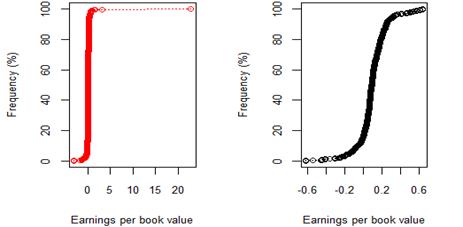
Figure 10. New York 8 year (2009-17) earnings per book value for rating category BBB before and after excluding companies identified as outliers
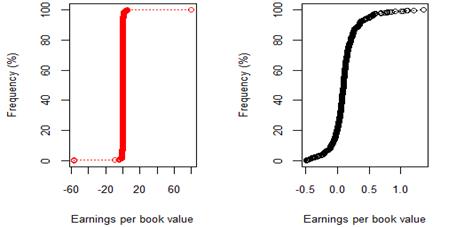
Figure 11. New York 8 year (2009-17) earnings per book value for rating category BB before and after excluding outliers
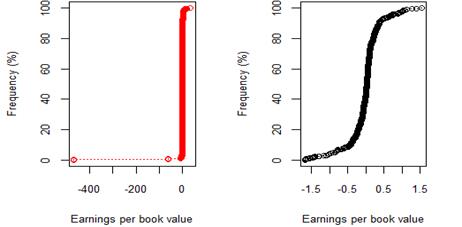
Figure 12. New York 8 year (2009-17) earnings per book value for rating category B before and after excluding companies identified as outliers
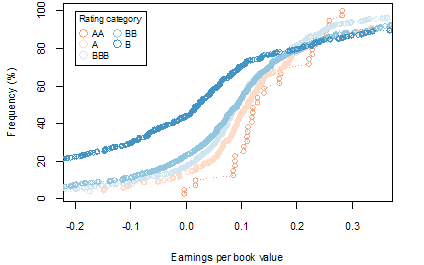
Figure 13. A comparison of NYSE 8 year (2009-17) earnings per book value by rating categories AA to B after excluding companies identified as outliers
Table 3. Summary statistics of NYSE earnings per book value by rating category
| NYSE data | AA | A | BBB | BB | B | |||||
| All data | After exclusions | All data | After exclusions | All | After exclusions | All data | After exclusions | All data | After exclusions | |
| No. of observations | 41 | 39 | 414 | 400 | 1103 | 1059 | 1232 | 1127 | 897 | 815 |
| Min | -0.0035 | -0.0035 | -0.8741 | -0.6157 | -2.9676 | -0.6157 | -56.4516 | -0.4913 | -466.3934 | -1.674 |
| 1st Quartile | 0.1038 | 0.1038 | 0.064 | 0.0634 | 0.03905 | 0.0422 | -0.0054 | 0.01955 | -0.1984 | -0.139 |
| Median | 0.1291 | 0.1291 | 0.1155 | 0.1117 | 0.0948 | 0.0948 | 0.089 | 0.0945 | 0.0193 | 0.0235 |
| Mean | 0.1611 | 0.1476 | 0.1597 | 0.1332 | 0.13458 | 0.1008 | 0.1019 | 0.11178 | -1.4176 | -0.01614 |
| 3rd Quartile | 0.2282 | 0.2246 | 0.1972 | 0.1887 | 0.1772 | 0.1741 | 0.1725 | 0.1731 | 0.1389 | 0.13625 |
| Interquartile range | 0.1244 | 0.1208 | 0.1332 | 0.1253 | 0.13815 | 0.1319 | 0.1779 | 0.15355 | 0.3373 | 0.27525 |
| Max | 0.4252 | 0.2808 | 2.1821 | 0.6991 | 22.848 | 0.6416 | 80.2768 | 1.3601 | 34.5146 | 1.5369 |
| Standard deviation | 0.0977 | 0.0787 | 0.2659 | 0.1651 | 1.0184 | 0.1530 | 4.0221 | 0.2180 | 22.6941 | 0.4397 |
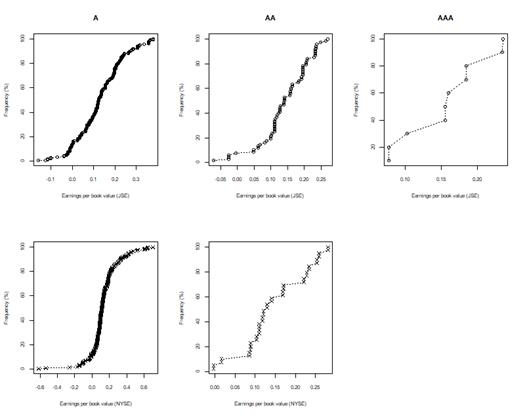
Figure 14. JSE and NYSE 8 year (2009-17) earnings per book value by rating categories A, AA and AAA after excluding companies identified as outliers
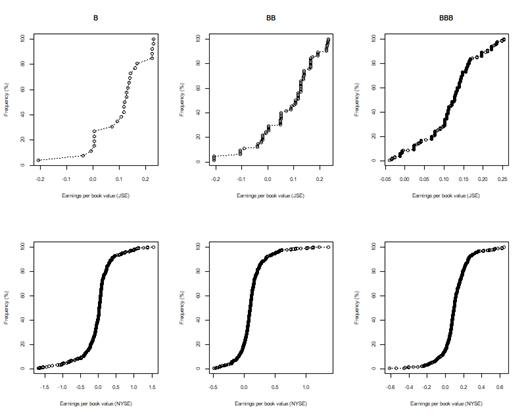
Figure 15. JSE and NYSE 8 year (2009-17) earnings per book value by rating categories B, BB and BBB after excluding companies identified as outliers
Table 4. Levene's test for equal variances in JSE earnings per book value
| Rating categories | Degrees of freedom | F Value | Pr (>F) |
| AAA and AA | 1 | 4.7571 | 0.0309 |
| AA and A | 1 | 30.192 | 6.36E-08 |
| A and BBB | 1 | 47.736 | 1.56E-11 |
| BBB and BB | 1 | 39.763 | 7.70E-10 |
| BB and B | 1 | 2.124 | 0.1469 |
| Overall | 5 | 24.098 | < 2.2e-16 |
Table 5. Two-sample T-test for equal means in JSE earnings per book value
| Welch's T-test | T-test | |||||
| AAA and AA | t = 0.70353 | df = 13.804 | p-value = 0.4934 | t = 0.58321 | df = 76 | p-value = 0.5615 |
| AA and A | t = 1.1278 | df = 157.08 | p-value = 0.2611 | t = 0.91547 | df = 307 | p-value = 0.3607 |
| A and BBB | t = 1.4172 | df = 408.37 | p-value = 0.1572 | t = 1.3567 | df = 437 | p-value = 0.1756 |
| BBB and BB | t = 3.0461 | df = 106.07 | p-value = 0.002925 | t = 3.7123 | df = 278 | p-value = 0.0002481 |
| BB and B | t = -1.0577 | df = 45.583 | p-value = 0.2958 | t = -1.0088 | df = 106 | p-value = 0.3154 |
Table 6. Levene's test for equal variances in NYSE earnings per book value
| Rating categories | Degrees of freedom | F Value | Pr (>F) |
| AA and A | 1 | 42.476 | 1.27E-10 |
| A and BBB | 1 | 0.3419 | 0.5588 |
| BBB and BB | 1 | 31.548 | 2.19E-08 |
| BB and B | 1 | 149.58 | < 2.2e-16 |
| Overall | 4 | 215.27 | < 2.2e-16 |
Table 7. Two-sample T-test for equal means in NYSE earnings per book value
| Welch's T-test | T-test | |||||
| AA and A | t = 0.95196 | df = 76.257 | p-value = 0.3441 | t = 0.53619 | df = 437 | p-value = 0.5921 |
| A and BBB | t = 3.4152 | df = 673.29 | p-value = 0.0006757 | t = 3.5341 | df = 1457 | p-value = 0.000422 |
| BBB and BB | t = -1.3703 | df = 2024.3 | p-value = 0.1708 | t = -1.3559 | df = 2184 | p-value = 0.1753 |
| BB and B | t = 7.6527 | df = 1103.8 | p-value = 4.277e-14 | t = 8.4376 | df = 1940 | p-value < 2.2e-16 |
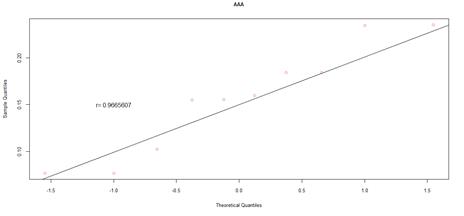
Figure 16. QQ plot comparing a theoretical normal distribution to that of rating category AAA earnings per book value JSE data after excluding companies identified as outliers
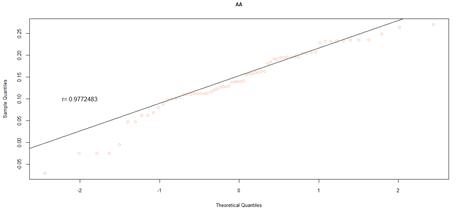
Figure 17. QQ plot comparing a theoretical normal distribution to that of rating category AA earnings per book value JSE data after excluding companies identified as outliers
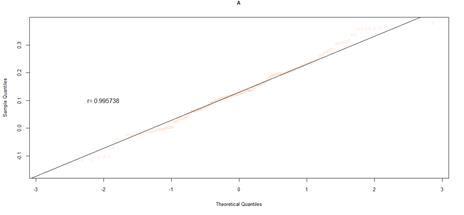
Figure 18. QQ plot comparing a theoretical normal distribution to that of rating category A earnings per book value JSE data after excluding companies identified as outliers
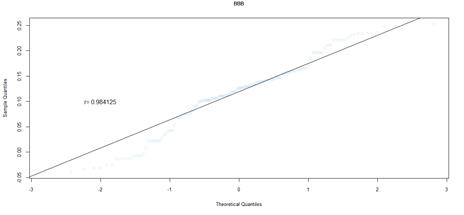
Figure 19. QQ plot comparing a theoretical normal distribution to that of rating category BBB earnings per book value JSE data after excluding companies identified as outliers
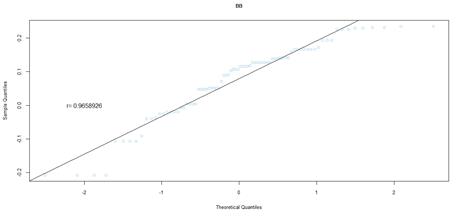
Figure 20. QQ plot comparing a theoretical normal distribution to that of rating category BB earnings per book value JSE data after excluding companies identified as outliers
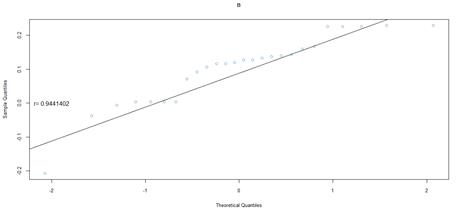
Figure 21. QQ plot comparing a theoretical normal distribution to that of rating category B earnings per book value JSE data after excluding companies identified as outliers
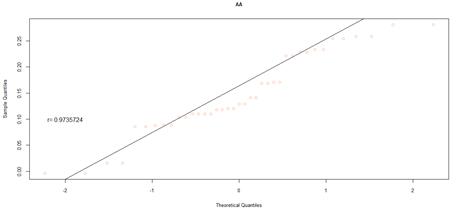
Figure 22. QQ plot comparing a theoretical normal distribution to that of rating category AA earnings per book value NYSE data after excluding companies identified as outliers
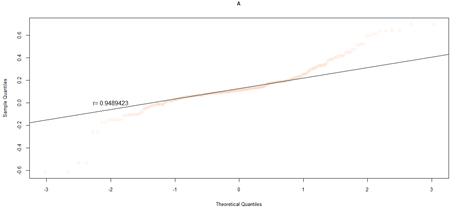
Figure 23. QQ plot comparing a theoretical normal distribution to that of rating category A earnings per book value NYSE data after excluding companies identified as outliers
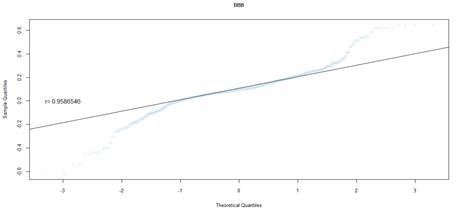
Figure 24. QQ plot comparing a theoretical normal distribution to that of rating category BBB earnings per book value NYSE data after excluding companies identified as outliers
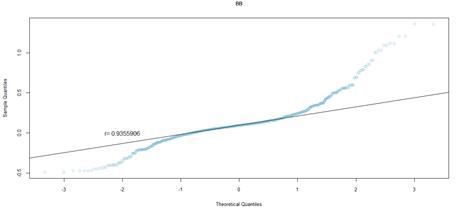
Figure 25. QQ plot comparing a theoretical normal distribution to that of rating category BB earnings per book value NYSE data after excluding companies identified as outliers
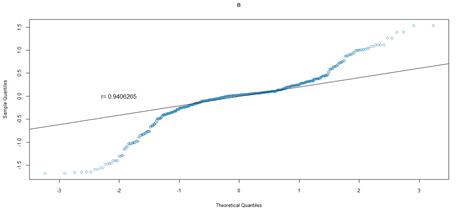
Figure 26. QQ plot comparing a theoretical normal distribution to that of rating category B earnings per book value NYSE data after excluding companies identified as outliers
5.2. Book Value Growth
To examine the second proposition and component of the study, book value growth distributions across rating categories were analysed for each market. The expectation was that, similar to earnings per book value, there would again be a consistent relationship between book value growth and rating category – a consistent relationship and pattern in book value growth across rating categories.
Year on year book value growth distributions of JSE listed companies and NYSE listed companies across all rating categories are illustrated in figures 27 and figure 35 respectively. The cumulative book value growth distributions of JSE listed companies across all rating categories are shown in figure 28, whilst figures 29 – 34 show the cumulative book value growth distributions of JSE listed companies of each rating category (AAA, AA, A, BBB, BB, B). The cumulative book value growth distributions of NYSE listed companies across all rating categories are shown in figure 36, whilst figures 37 – 41 show the cumulative book value growth distributions of NYSE listed companies of each rating category (AAA, AA, A, BBB, BB, B). The summary statistics of the book value growth distributions of JSE and NYSE listed companies by rating category are presented in tables 8 and 11 respectively.
Table 9 and Table 12 show the results of Levene’s test performed on the JSE and NYSE data respectively, to test whether variances of book value growth are equal across rating categories. A two-sample T-test for equal means of book value growth is presented in tables 10 and 13, for the JSE and NYSE data respectively. The probabilities of book value growth for JSE and NYSE listed companies by rating category are presented in tables 14 and 15 respectively. This entails the probability of either positive or negative book value growth, the probability of positive book value growth, the probability of negative book value growth, and the probability of no book value growth (book value remaining the same).
5.2.1. Inferences from the Descriptive Statistics
It was expected that book value growth would demonstrate a consistent relationship across rating categories. Part of the expectation was that higher quality rating categories would display more consistent growth rates, whilst speculative rating categories would show more volatile growth rates.
However, the JSE data set shows loose relationships, inconsistent with expected results. There appears to be more frequent growth for companies in the speculative rating categories, compared to higher quality rating categories, as shown by the maximum values and interquartile ranges of book value growth in table 8. Nevertheless, this pattern does not seem to hold, with some lower quality rating categories, such as BBB, behaving like higher quality rating categories, and vice versa. The volatility was further confirmed by the overall probabilities of book value growth, as shown in table 14. Rating category AA, followed by rating category BBB, are most likely to experience book value growth. Rating category A has the least probability of experiencing any type of book value growth – positive or negative. The overall probabilities of book value growth are similar for ratings AAA and BBB. Based on the likelihood for positive book value growth, rating categories AAA, AA and BB show close similarities. These 3 rating categories, and in addition rating category BBB, are more or less twice as likely to experience positive book value growth, than negative growth in book value.
In contrast, the NYSE dataset shows patterns per rating category and across rating categories that differ from the JSE dataset. The higher quality rating categories are generally more stable, and as ratings move towards more speculative grades, the book value growth become more volatile. As shown in table 15, rating categories AA, BBB and BB are all most likely to experience any kind of – positive or negative - book value growth. In terms of positive growth, rating categories A and B are similar to each other, in that they both show similar likelihood of positive or negative growth. Rating categories BBB and BB are approximately 4 times more likely to experience positive rather than negative book value growth. As shown in table 11, there is an increase in the maximum values of book value growth across rating categories, except for rating category BB. Lower quality rating categories show more growth potential, and it can be taken that they demonstrate greater risk potential. Higher quality rating categories that are more stable, show less risk potential, but appear to experience more negative book value growth, possibly related to and suggesting rating downgrades and restructuring.
5.2.2. Statistical Tests
Levene’s test was performed to test for differences in variance of book value growth across rating categories, for both the JSE and NYSE datasets. The null hypothesis was that the variance in the book value growth distributions across rating categories are equal.
For the JSE market, variance of book value growth is equal only across rating categories AAA and AA. However, for the NYSE market, variance of book value growth is equal across all rating categories, except across rating categories AA and A.
Welch’s T-test was therefore considered the appropriate statistical test to establish the difference in means of book value growth across rating categories: For the JSE data, Welch’s T-test was used across all rating categories, except across ratings AAA and AA, where the standard T-test was used. The p values of Welch’s T-test were found to be significant across rating categories A and BBB, and across rating categories BB and B. For the NYSE data, the standard T-test was appropriate to use, except across rating categories AA and A. The T-test was found to be significant across rating categories A and BBB, and across rating categories BB and B. This is similar to the pattern displayed by the JSE data.
5.2.3. Conclusion
Similar to earnings to book value, the smaller JSE market and sample also appears to approximate the larger NYSE market and sample, when it comes to book value growth. However, or still, a closer examination of the probability of book value growth across the 2 markets show inconsistent patterns. More data – a greater sample – may be needed, to further shed light on this.
Also very relevant to equity valuation, book value growth can of course be both positive and negative. Book value may increase or decrease. This may imply and introduce both earnings growth and contraction, and book value growth may move both with and contrary to earnings growth. In essence, it implies a more complex relationship than what contemporary valuation models consider, encapsulate and incorporate.
The results also indicate that book value changes are not completely random. Even though book value growth do not truly demonstrate a consistent pattern across rating categories, individual rating categories reveal distinct book value growth patterns, and these can be examined in greater depth.
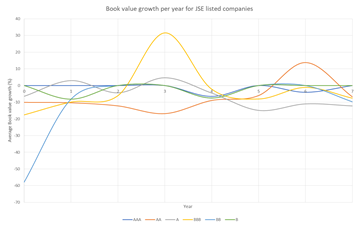
Figure 27. Average book value growth distributions year on year for JSE listed companies
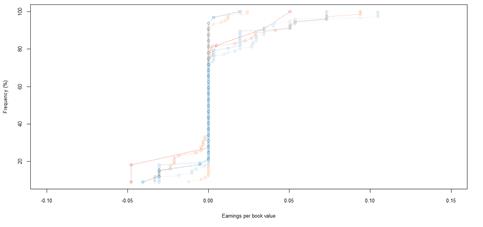

Figure 28. Book value growth distributions for JSE listed companies by rating category
Table 8. Summary statistics of the book value growth distributions for JSE listed companies by rating category
| JSE data | AAA | AA | A | BBB | BB | B |
| No. of observations | 10 | 68 | 241 | 198 | 82 | 26 |
| Min | -0.0479 | -0.0331 | -0.0123 | -0.0331 | -0.0306 | -0.0406 |
| 1st Quartile | 0 | -0.0022 | 0 | 0 | 0 | 0 |
| Median | 0 | 0 | 0 | 0 | 0 | 0 |
| Mean | -0.0005727 | 0.005246 | 0.000859 | 0.009401 | 0.005737 | -0.002813 |
| 3rd Quartile | 0.0024 | 0.0005 | 0 | 0.0096 | 0.0032 | 0 |
| Interquartile range | 0.0024 | 0.0027 | 0 | 0.0096 | 0.0032 | 0 |
| Max | 0.0503 | 0.0938 | 0.0241 | 0.1046 | 0.073 | 0.0194 |
| Standard deviation | 0.0288 | 0.0272 | 0.0044 | 0.0255 | 0.0239 | 0.0113 |
Table 9. Levene's test for equal variances in the book value growth of JSE listed companies
| Rating categories | Degrees of freedom | F Value | Pr (>F) |
| AAA and AA | 1 | 0.153 | 0.6963 |
| AA and A | 1 | 57.943 | 2.37E-13 |
| A and BBB | 1 | 36.158 | 4.45E-09 |
| BBB and BB | 1 | 0.6183 | 4.32E-01 |
| BB and B | 1 | 9.3076 | 0.0027 |
| Overall | 5 | 18.275 | < 2.2e-16 |
Table 10. Two-sample T-test for equal means in the book value growth of JSE listed companies
| Welch's T-test | T-test | |||||
| AAA and AA | t = -0.62372 | df = 13.189 | p-value = 0.5434 | t = -0.65066 | df = 74 | p-value = 0.5173 |
| AA and A | t = 1.2942 | df = 65.184 | p-value = 0.2002 | t = 2.108 | df = 245 | p-value = 0.03604 |
| A and BBB | t = -4.2151 | df = 170.51 | p-value = 4.041e-05 | t = -4.4407 | df = 343 | p-value = 1.211e-05 |
| BBB and BB | t = 1.0547 | df = 141.6 | p-value = 0.2934 | t = 1.028 | df = 232 | p-value = 0.305 |
| BB and B | t = 2.4361 | df = 97.72 | p-value = 0.01666 | t = 1.8668 | df = 99 | p-value = 0.06489 |
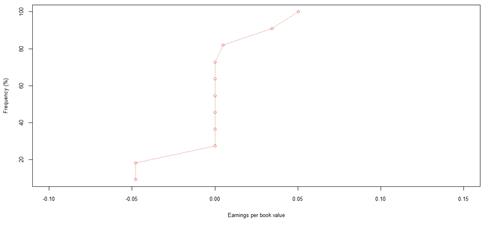
Figure 29. Book value growth distributions for JSE listed companies by rating category AAA
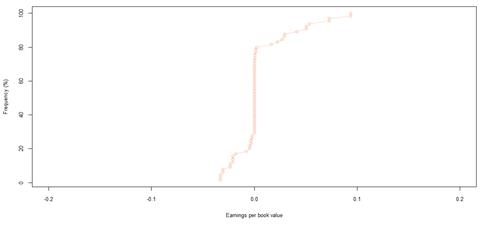
Figure 30. Book value growth distributions for JSE listed companies by rating category AA
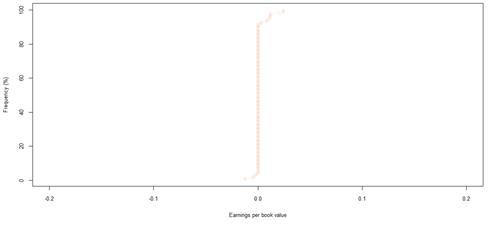
Figure 31. Book value growth distributions for JSE listed companies by rating category A
Figure 32. Book value growth distributions for JSE listed companies by rating category BBB
Figure 33. Book value growth distributions for JSE listed companies by rating category BB
Figure 34. Book value growth distributions for JSE listed companies by rating category B
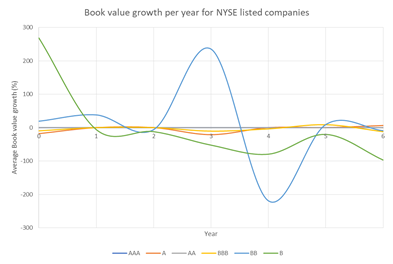
Figure 35. Average book value growth distributions year on year for NYSE listed companies
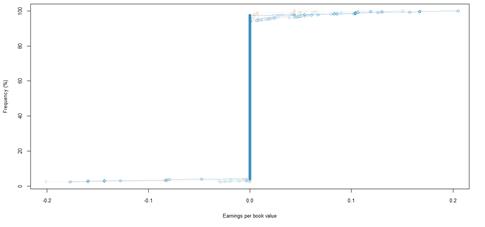

Figure 36. Book value growth distributions for NYSE listed companies by rating category
Table 11. Summary statistics of the book value growth distributions for NYSE listed companies by rating category
| AA | A | BBB | BB | B | |
| No. of observations | 39 | 400 | 1059 | 1127 | 815 |
| Min | -0.0591 | -0.5667 | -0.0309 | -0.0317 | -0.1993 |
| 1st Quartile | 0 | 0 | 0 | 0 | 0 |
| Median | 0 | 0 | 0 | 0 | 0 |
| Mean | -0.0000919 | -0.006267 | 0.00946 | 0.1087 | 0.00067 |
| 3rd Quartile | 0 | 0 | 0 | 0 | 0 |
| Interquartile range | 0 | 0 | 0 | 0 | 0 |
| Max | 0.0437 | 0.1328 | 0.1628 | 0.1506 | 0.2052 |
| Standard deviation | 0.0175 | 0.0558 | 0.0282 | 0.0303 | 0.0465 |
Table 12. Levene's test for equal variances in the book value growth of NYSE listed companies
| Rating categories | Degrees of freedom | F Value | Pr (>F) |
| AA and A | 1 | 7.8424 | 0.0052 |
| A and BBB | 1 | 1.8457 | 0.1744 |
| BBB and BB | 1 | 1.0835 | 0.2980 |
| BB and B | 1 | 2.9336 | 0.0869 |
| Overall | 4 | 8.2872 | 1.17E-06 |
Table 13. Two-sample T-test for equal means in the book value growth of NYSE listed companies
| Welch's T-test | T-test | |||||
| AA and A | t = 1.5336 | df = 126.76 | p-value = 0.1276 | t = 0.66984 | df = 428 | p-value = 0.5033 |
| A and BBB | t = -5.7507 | df = 490.29 | p-value = 1.566e-08 | t = -7.2405 | df = 1342 | p-value = 7.504e-13 |
| BBB and BB | t = -1.0472 | df = 1885.2 | p-value = 0.2952 | t = -1.0469 | df = 1893 | p-value = 0.2953 |
| BB and B | t = 5.1721 | df = 1203.3 | p-value = 2.71e-07 | t = 5.4415 | df = 1688 | p-value = 6.059e-08 |
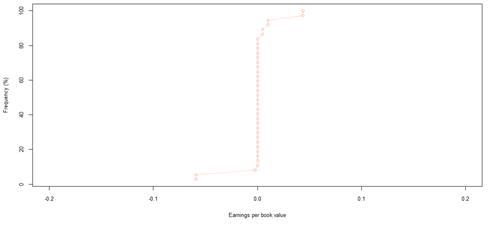
Figure 37. Book value growth distributions for NYSE listed companies by rating category AA
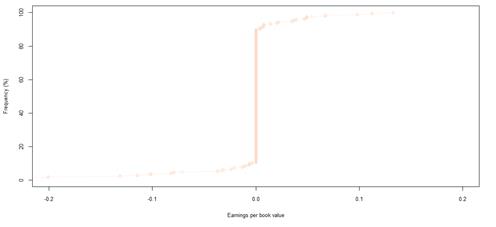
Figure 38. Book value growth distributions for NYSE listed companies by rating category A
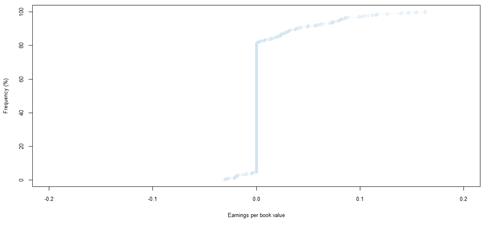
Figure 39. Book value growth distributions for NYSE listed companies by rating category BBB
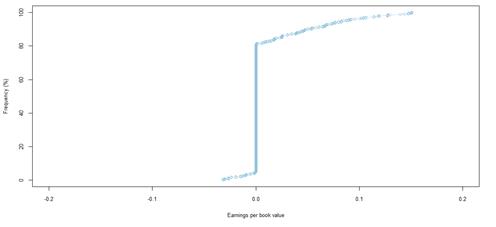
Figure 40. Book value growth distributions for NYSE listed companies by rating category BB
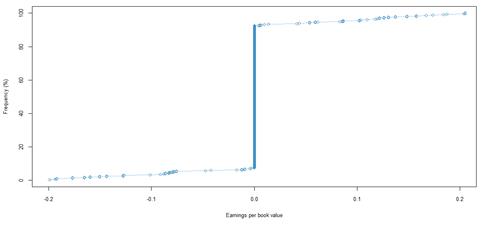
Figure 41. Book value growth distributions for NYSE listed companies by rating category B
Table 14. Probabilities of book value growth for JSE listed companies by rating category
| Rating | Positive or negative growth | Positive growth | Negative growth | No (zero) growth |
| AAA | 45% | 27% | 18% | 55% |
| AA | 55% | 28% | 28% | 45% |
| A | 13% | 9% | 4% | 87% |
| BBB | 49% | 33% | 17% | 51% |
| BB | 39% | 27% | 13% | 61% |
| B | 20% | 7% | 13% | 80% |
Table 15. Probabilities of book value growth for NYSE listed companies by rating category
| Rating | Positive or negative growth | Positive growth | Negative growth | No (zero) growth |
| AA | 24% | 16% | 8% | 76% |
| A | 21% | 10% | 10% | 79% |
| BBB | 24% | 19% | 5% | 76% |
| BB | 24% | 19% | 5% | 76% |
| B | 15% | 8% | 7% | 85% |
6. Conclusion
The results of the study generally support the proposition that earnings to book value are comparable per rating category, and distinct across rating categories. Although perhaps not as significant or strong as desired, there is a clear and consistent relationship in earnings to book value across rating categories. Earnings to book value distributions of rating categories are also generally distinct, approximating normal distributions.
Book value growth demonstrated less of a consistent relationship across rating categories. Rather, very individual and specific relationships or patterns of book value growth were demonstrated per rating category.
The relationship between book value growth and rating category points to and returns to equity valuation intricacies and complexities. The relationship and patterns between book value growth and rating category should be further studied, in order to build more comprehensive valuation models. It (studies) should be possible (able) to explain the individual and specific relationships and patterns book value growth demonstrates per rating category.
Both the results of the relationship between earnings per book value and rating category, and the relationship between book value growth and rating category, equally bring to the surface the issue of the accuracy of ratings. Should both earnings per book value, and book value growth each have clear and consistent relationships across rating categories? In the case that they don’t, does it imply that ratings assigned are inaccurate?
Although consistent relationships of earnings to book value, and book value growth, across rating categories may be sensible and thus desirable, valuation models that build on and incorporate these, like the proposed valuation model, do not truly require that earnings to book value, and book value growth, are consistent in relationship across rating categories, only that earnings to book value, and book value growth, are consistent, and known to be consistent per rating category. Thus, the consistency of the earnings to book value, and book value growth distributions becomes important.
Although generally limited in the case of earnings to book value, and really only moderate in the case of book value growth, the degree of randomness resident in the earnings to book value, and book value growth distributions, may be an alternative perspective and vantage point on the degree of uncertainty present in equity markets and equity valuations, that is by definition unavoidable. Thus, the accuracy that valuation models that build on these distributions, can achieve, would be insightful.
The small sample size of the JSE dataset reduced the ability to detect clear patterns, and was a real obstacle to more reliable analysis of that market. In general, the JSE dataset approximated the results obtained for the NYSE dataset, which had a larger sample size. A larger sample size and sampling interval may allow trends to be better observed. Only the major rating categories were considered, but a more comprehensive study can cover the full range of rating categories, with a more extensive dataset.
6.1. Future Research
Future research can look at the following:
· The full range of rating categories can be considered, with a more extensive dataset. The study only examined the major rating categories, and a larger sample size and sampling interval can be used.
· The consistency of the earnings to book value, and book value growth distributions are important, and can be further investigated.
· Outliers in earnings to book value and book value growth distributions should be further examined and explained. The study simply excluded these, without studying them in greater depth.
· The relationship and patterns between book value growth and rating category can be further studied. The individual and specific relationships and patterns book value growth demonstrates per rating category can be investigated in depth.
· The relationship between earnings to book value and rating category, and the relationship between book value growth and rating category, in the context of accuracy of ratings, can receive more attention. Should earnings to book value, and book value growth, have consistent relationships with and across rating categories?
· The accuracy of valuation models that build on and incorporate earnings to book value and book value growth distributions can be established. Also, the actual earnings and book value probability distributions of a firm, and even a market, can be modelled and simulated. This was outside of the scope of this study.
References
- Altman, E. I., 1989. Measuring corporate bond mortality and performance. The Journal of Finance, 44(4), pp.909-922.
- Altman, E. I., 1996. Rating Migration of Corporate Bonds: Comparative Results and Investor/Lender Implication. Working paper, Stern School of Business.
- Bangia, A., Diebold, F. X., Kronimus, A., Schagen, C. and Schuermann, T., 2002. Ratings migration and the business cycle, with application to credit portfolio stress testing. Journal of Banking & Finance, 26(2), pp.445-474.
- Cantor, R. and Packer, F., 1996. Determinants and impact of sovereign credit ratings. The Journal of Fixed Income, 6(3), pp.76-91.
- Chen, P. and Zhang, G., 2007. How do accounting variables explain stock price movements? Theory and evidence. Journal of Accounting and Economics, 43(2), pp.219-244. doi: 10.1016/j.jacceco.2007.01.001
- Courteau, L., Kao, J. L. and Richardson, G. D., 2001. Equity valuation employing the ideal versus ad hoc terminal value expressions. Contemporary accounting research, 18(4), pp.625-661.
- Damodaran, A., 2007. Valuation approaches and metrics: a survey of the theory and evidence. Foundations and Trends in Finance, 1(8), pp.693-784.
- De Haan, J. and Amtenbrink, F., 2011. Credit rating agencies. [online] Available at: https://www.dnb.nl/en/binaries/Working%20Paper%20278_tcm47-246556.pdf [Accessed on 11 January 2019].
- Erdem, O. and Varli, Y., 2014. Understanding the sovereign credit ratings of emerging markets. Emerging Markets Review, 20 (Supplement C), pp.42-57. doi: 10.1016/j.ememar.2014.05.004
- Fei, F., Fuertes, A. M. and Kalotychou, E., 2012. Credit rating migration risk and business cycles. Journal of Business Finance & Accounting, 39(1‐2), pp.229-263.
- Fernandez, P., 2001. Valuation using multiples. How do analysts reach their conclusions? IESE Business School, 1, pp.1-13.
- Fernandez, P., 2007. Valuing companies by cash flow discounting: ten methods and nine theories. Managerial Finance, 33(11), pp.853-876.
- Frydman, H. and Schuermann, T., 2008. Credit rating dynamics and Markov mixture models. Journal of Banking & Finance, 32(6), pp.1062-1075.
- Gonzalez, F., Haas, F., Persson, M., Toledo, L., Violi, R., Wieland, M. and Zins, C., 2004. Market dynamics associated with credit ratings: a literature review.
- Hill, P. and Faff, R., 2010. The Market Impact of Relative Agency Activity in the Sovereign Ratings Market. Journal of Business Finance & Accounting, 37(9/10), pp.1309-1347. doi:10.1111/j.1468-5957.2010.02220.x
- Jarrow, R. A., Lando, D. and Turnbull, S. M., 1997. A Markov Model for the Term Structure of Credit Risk Spreads. The Review of Financial Studies, 10(2), pp.481-523.
- Jarrow, R. A. and Turnbull, S. M., 1995. Pricing Derivatives on Financial Securities Subject to Credit Risk. The Journal of Finance, 50(1), pp.53-85. doi:10.2307/2329239
- Kadam, A. and Lenk, P., 2008. Bayesian inference for issuer heterogeneity in credit ratings migration. Journal of Banking & Finance, 32(10), pp.2267-2274.
- Kisgen, D. J., 2006. Credit Ratings and Capital Structure. The Journal of Finance, 61(3), 1035-1072. doi:10.1111/j.1540-6261.2006.00866.x
- Kormos, B. J., 2008. Quis Custodiet Ipsos Custodes? Revisiting Rating Agency Regulation. International Business Law Journal, 4, pp. 569–590.
- Lando, D. and Skødeberg, T. M., 2002. Analyzing rating transitions and rating drift with continuous observations. Journal of Banking & Finance, 26(2), pp.423-444.
- Mählmann, T., 2009. Multiple Credit Ratings, Cost of Debt and Self‐Selection. Journal of Business Finance & Accounting, 36(9‐10), pp.1228-1251.
- Nickell, P., Perraudin, W. and Varotto, S., 2000. Stability of rating transitions. Journal of Banking & Finance, 24(1), pp.203-227.
- Nissim, D. and Penman, S. H., 2001. Ratio analysis and equity valuation: From research to practice. Review of accounting studies, 6(1), pp.109-154.
- Penman, S. H., 1998a. Combining earnings and book value in equity valuation. Contemporary accounting research, 15(3), 291-324.
- Penman, S. H., 1998b. A synthesis of equity valuation techniques and the terminal value calculation for the dividend discount model. Review of accounting studies, 2(4), pp.303-323.
- Penman, S. H., 2001. On comparing cash flow and accrual accounting models for use in equity valuation: A response to Lundholm and O'Keefe (CAR, Summer 2001. Contemporary accounting research, 18(4), pp.681-692.
- Penman, S. H. and Sougiannis, T., 1998. A comparison of dividend, cash flow, and earnings approaches to equity valuation. Contemporary accounting research, 15(3), pp.343-383.
- R Core Team, 2018. R: A language and environment for statistical computing (Version 1.1453). Vienna, Austria: R Foundation for Statistical Computing.
- Reiter, S. A. and Ziebart, D. A., 1991. Bond yields, ratings, and financial information: Evidence from public utility issues. Financial Review, 26(1), pp.45-73.
- Ross, S. A., Westerfield, R., Jordan, B. D. and Firer, C., 2000. Fundamentals of corporate finance: Irwin/McGraw-Hill Boston, MA.
- Rowland, P., 2005. Determinants of spread, credit ratings and creditworthiness for emerging market sovereign debt: a follow-up study using pooled data analysis. Borradores de Economia No, 296, pp.1-37.
- Steiger, F., 2010. The validity of company valuation using Discounted Cash Flow methods. arXiv preprint arXiv:1003.4881.
- Tusa, F., 2016. Credit Rating Agencies. In: Erişim Tarihi.
- Zhang, G., 2000. Accounting Information, Capital Investment Decisions, and Equity Valuation: Theory and Empirical Implications. Journal of Accounting Research, 38(2), pp.271-295. doi:10.2307/2672934
Article Rights and License
© 2019 The Authors. Published by Sprint Investify. ISSN 2359-7712. This article is licensed under a Creative Commons Attribution 4.0 International License.


