Keywordshealth insurance healthcare seeking behavior moral hazard optimal consumption-leisure choice
JEL Classification D11, D81, I13
Full Article
1. Introduction
While the history of the problem of moral hazard goes back to the 17th century, its scientific analysis started only in the last century, when Kenneth Arrow published his prominent article on health insurance. That article opened the wide discussion in economics and law. “Rivers of ink have been spilled discussing the moral hazard problem of insurance and ways to mitigate it.”(Ben-Shahar and Logue 2012, p.199). As usual, applied economics grew faster than its theoretical basis. Nevertheless, works of M.Pauly, J.Stiglitz, M.Spence and R.Zeckhauser developed the theory of ideal insurance, proposed by Arrow. In 2009 Zwietfel et al. in “Health Economics” had summarized microeconomic visions of the moral hazard in health insurance.
The standard microeconomic analysis of the phenomenon of moral hazard focuses on the consumer’s wealth under the expected utility. The theory of the optimal consumption-leisure choice under price dispersion can propose an interesting extension to the traditional microeconomic vision of the moral hazard with the set of assumptions of the present utility. The optimal consumer choice depends on the search for low prices. In health insurance the price of contract depends on customers’ precautionary efforts. While the price discrimination in the health industry is strictly regulated and sometimes prohibited, there are some ways for insurers to motivate the riskless behavior and to propose lower prices for careful applicants. People can stop smoking, they can undertake health-enhancing activities in gyms and pools, and finally they can choose medical underwriting in order to provide the information for insurance companies and to decrease payments. The propensity to search, the key variable of the model of optimal search, takes the form of the propensity to seek healthcare.
However, even healthcare seeking behavior does not eliminate moral hazard, which, in its ex post form of the increase in demand for medical services, stays the most statistically significant phenomenon (Zwietfel and Manning, 2000). The model of the optimal consumption-leisure choice under price dispersion enlightens some microeconomic mechanisms of moral hazard and tries to dispel the illusion of “unlimited demand for free medical services” that follows the phenomenon of moral hazard in economic literature.
2. Price Dispersion in Health Insurance
The understanding of the phenomenon of moral hazard as a specific form of the optimal consumption-leisure choice needs the reassignment of the standard set of variables to the case of health insurance. Here we have the problem maxU(Q,H) subject to w/∂P/∂S|const=Q/∂L/∂S, where the value w represents the given wage rate, the value ∂P/∂Sconst<0 represents the given price discount, which depends on healthcare activities, the value of consumption Q represents a medical service under the insurance claim, and the variable ∂L/∂S<0 represents the propensity to seek healthcare, i.e., propensity to substitute labor L for healthcare activities S, where the time horizon T until the next payment or purchase is equal to L+S+H. The (Q,H) utility is maximized when:
![]()
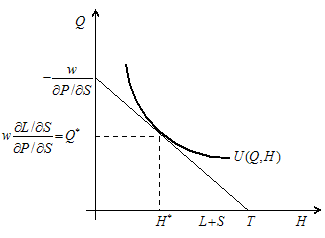
Figure 1. Optimal consumption-leisure choice under price disperdion.
The modern economic theory presents the first-best insurance contract as the full insurance that also requires some precautionary observable effort e. The model of the optimal consumption-leisure choice supports that conclusion but it adds some important remarks.
While the modern economic theory insists on the tangibility of the precautionary effort, i.e., this effort should represent either direct expenditures or the monetary equivalent of the disutility of the effort itself, the model of the optimal consumption-leisure choice pays attention to the fact that monetary equivalent of the precautionary effect depends on income, here on the wage rate. Thus, the time spent on this effort should be different for different levels of the wage rate. The same thing should happen with the price for the insurance contract.
Then, if a precautionary effort is costly, these should be always a trade-off between costs on healthcare seeking and a price of purchase. Hence there should be a price with zero precautionary effort. At the optimal level the marginal cost of the precautionary effort should equal its marginal benefit. The model of the optimal consumption-leisure choice pays attention to the fact that at some level of income w, price of purchase QP=wL, and the price reduction ∂P/∂S, there is an optimal solution with zero healthcare seeking costs S:
![]()
Here the individual chooses the lowest level of precautionary effort e=0.
If healthcare-seeking behavior represents a particular form of search for low prices, the competitive market takes the shape of the equilibrium price dispersion (Malakhov, 2016) where consumers with different propensities to seek healthcare and therefore different willingness to pay for the insurance policy meet different fair insurance policies (Fig.2)
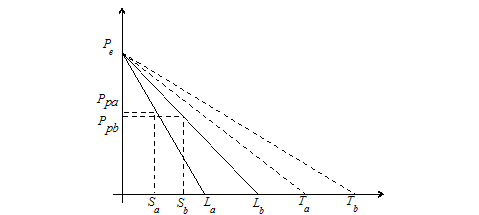
Figure 2. Equilibrium price disperdion.
Let’s take Figure 2 as the illustration of the equilibrium price dispersion for the full coverage Q=1. We see that people with different income spend different labor time L in order to buy the full coverage as well as they spent different time S for healthcare seeking, i.e., for precautionary efforts. The competition between insurers enforces them to meet customers’ different willingness to pay and to take into account different time spent on the purchase of full coverage. And insurance companies propose policies with different time horizons.
The equilibrium price dispersion follows the transformation of the Equation 1:
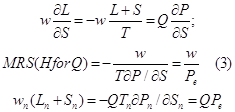
Here all purchase prices QPn=wnLn represent derivative values of one equilibrium price. The equilibrium price equals to the full coverage policy for people with zero healthcare seeking costs S. Other words, it equals to the willingness to pay of a consumer who a) does not want to waste time on precautionary efforts; b) does not care about his health, and, c) cannot make precautionary efforts.
The logic of the model also needs the equality of that willingness to pay with the willingness to accept or to sell of another consumer who undertakes health-enhancing activities and who seeks for healthcare. Indeed, if total costs of the insurance policy, labor time for the purchase itself and the time for precautionary efforts, exceed the equilibrium price, a consumer can stop health-enhancing activities; he can reject the medical underwriting and buy the full coverage at the equilibrium price level. Finally, unsatisfied consumer can quit the market uninsured when he meets a take-it-or-leave-it offer. It means that the insurance company should propose for careful consumers fair policies that take into account efforts on healthcare. Unfortunately, while consumers are price-takers, they depend on insurers’ ability to gather accurate information about these efforts of insurance applicants. If the information is collected properly, consumers can expect fair prices and they do not need additional efforts on healthcare. We suppose that these additional efforts, ambulatory care visits to physician offices and hospitals, named ex post moral hazard, take place when the insurance policy is unfair.
The question why insurance contracts could be unfair needs very detailed applied analysis. They are administrative costs, costs of investment management and some other overheads that increase premiums. That analysis is left beyond this paper, which pays its attention to the consumers’ reaction on unfair policy. And the starting point for the analysis of consumers’ reaction on unfair price is clear. Even Arrow had to admit the fact that when consumers were risk-averse they could accept slightly unfair premiums: “From the point of view of the individual, since he has a strict preference for the actuarially fair policy over assuming the risks himself, he will still have a preference for an actuarially unfair policy, provided, of course, that it is not too unfair.” (Arrow 1963, p.960).
3. Moral Hazard as the Process of Optimization
There are some important notions that stay beyond the key equation of the model. First, we should precise the allocation of time for a good named “insurance policy”. A consumer needs labor time L in order to buy a policy and to get indirect access to medical services. Then he spends some time S on healthcare that, as he thinks, makes the access to medical services cheaper. The comparative statics divides the value of healthcare seeking behavior into ex ante healthcare efforts and ex post activities. In the “common model” of behavior (see Malakhov 2015) these activities decrease not only the labor time L but also leisure time H. Indeed, visits to hospitals reduce our leisure. The case of physical training in gyms and pools is more complicated, while such activities could be regarded as leisure. Here we meet a black box of the modern theory of allocation of time, which cannot present for the moment a satisficing methodology for the analysis of such “dual activities”, like gardening, pet care, etc. that can be treated as non-market activities as well as leisure (see Aguiar and Hurst 2007). However, the model of optimal healthcare seeking behavior can override this methodological barrier. Buying the insurance policy, a consumer gets a specific form of leisure. This is tranquility, the quiet state when he does not bother about his health. Thus, the time of leisure of a good “insurance policy” includes the working time, search, and leisure for all other goods. From this point of view the time in gyms and pools really represents a form of healthcare. As a result, buying an insurance policy, a consumer tries to maximize the utility of quiet state H and of an access to medical treatment Q.
The price reduction ∂P/∂S can be got only by the confirmation of ex ante healthcare activities. When the insurance contract is signed, if it does not specify some ex post activities, ex post healthcare-seeking behavior cannot change both the price and its corresponding discount. And under the contract the marginal precautionary effort takes the following form (Eq.4):
![]()
The consumer does not calculate marginal values. But it might be not true for the insurance company. A provider who tries to understand customer’s willingness to pay and to make precautionary efforts has enough means even to re-construct the individual propensity to seek healthcare, But if the information is asymmetric, the insurer can miss some hidden action of healthcare and the evaluation of the precautionary effort Scontract will be less than the actual healthcare seeking behavior Sex ante, and the offer will be definitely unfair. However, from the point of view of the equilibrium price dispersion the unfair policy, even if its slightly unfair, means that total costs of the careful applicant for the access to medical treatment Q are greater than the equilibrium expenditures, or
![]()

Figure 3. Purchase of unfair insurance policy.
If we re-arrange the Equation 5, we get the following result:
![]()
or the absolute value of marginal costs of purchase are greater than the absolute value of its marginal benefit.
When the values of price discount ∂P/∂S and the time horizon of the insurance policy T are fixed with the purchase, for the given wage rate w we get the line of budget constraint and the hypothetical optimal consumer choice at the point C of the utility of contract UC (Fig.3):
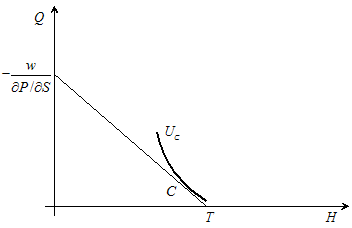
Figure 4. Hypoyhetical optimal choice of unfair insurance policy.
But this choice is really hypothetical. The inequality of marginal values, presented in Equation 6, disperse this illusion of optimality:
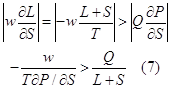
or the utility curve at the point C is flatter than the budget constraint. And we get the suboptimal solution (Fig.5):
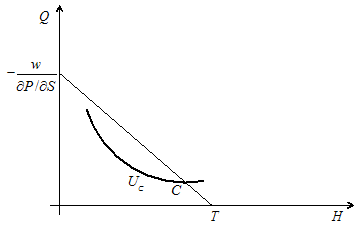
Figure 5. Suboptimal consumption-leisure choice under unfair insurance policy.
The unfair policy means that the insurance contract is not optimal. The Equation 6 tells us that either the purchase price PC is too high due to some overhead costs, or the insurance company underestimates ex ante healthcare activities. Thus, the offer becomes unfair from the point of view of the applicant.
But the consumer can adjust the contract to his needs and get the satisficing as well as optimal solution (The analysis of the transformation of explicit satisficing decision into implicit optimal solution is presented in Malakhov (2014) and Malakhov (2016)). When the budget constraint is given, he can move along it in the north-west direction. When the labor time L ix fixed by the purchase, the individual substitutes the time of leisure H by healthcare seeking Sex post (here do not forget about specificity of “leisure” under insurance policy, it might be working and searching time, and the time of enjoyment of other goods). The consumer does not calculate marginal values. He simply searches for the satisficing solution. For example, people can seek early treatment in order to avoid hospitalization in future. And this decision becomes optimal when consumer increases access to medical treatment Q. He begins to visit physicians. As a result he raise the utility level of the insurance contract UC to the level of moral hazard utility UMH (Fig.6):
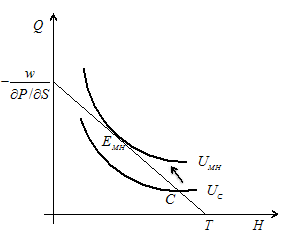
Figure 6. Moral hazard.
Indeed, the consumer increases the intensity of consumption Q/H proposed by the insurance policy. And his visits to physicians become more frequent. The consumer increases the absolute value of the marginal propensity to seek health care because in the static world he can get the following satisficing optimal result (If the contract specifies some ex post observable activities like clinical examination, the consumer can increase both the consumption of extra medical services as well as the the total Sex post time for such activities):
![]()
From the first point of view it looks like a paradox. Why the consumer substitutes leisure for visits to physicians when total costs of healthcare are already high? The answer is in the simple mathematics. Let’s suppose that healthcare activity S represents the number of physicians’ visits Q times the duration of one visit. The consumer accepts the medical underwriting and he confirms the state of his health ex ante by some medical analysis. Being unsatisfied with the contract, he continues to visit physicians, now ex post under the insurance. Thus, he increases both Sex post and Qex post values. However, the Equations 1-3 show us that when the values of S and Q are increasing at the same rate, the absolute value of marginal benefits |Q∂P/∂Sconst| is growing faster than the absolute value of marginal costs |w∂L/∂S|. Thus, the arrival to the optimal choice EMH under moral hazard is inevitable.
Here we can see that the phenomenon of moral hazard does not represent an “unlimited demand for free goods”. Leaving the point C of the unfair policy, the consumer stops at the point EMH. The marginal rate of substitution of leisure for consumption (MRS H for Q) at the point C of the utility curve UC is too low. There are too much leisure (MUL is low) and a deficit of consumption (MUC is great). Moving from C to EMH, the individual decreases the time of leisure and increases the consumption. Thus, the MRS H for Q is rising. But this value cannot grow infinitely. Once the individual understands that he has sacrificed enough leisure for medical treatment. The best illustration of the moral hazard as the process of optimization can be found in the article “The Moral-Hazard Myth”, written by M.Gladwell for The New Yorker where he cited U.Reinhardt, professor of political economy in Princeton University and the prominent scholar in healthcare economics: “Moral hazard is overblown…You always hear that the demand for health care is unlimited. This is just not true. People who are very well insured, who are very rich, do you see them check into the hospital because it’s free? Do people really like to go to the doctor? Do they check into the hospital instead of playing golf?”(Gladwell, 2005).
Here U.Reinhardt pays attention to the income level that reduces moral hazard. This is only a part of the story, but it is very important. We see that the reason for moral hazard is hidden in the high absolute value of marginal losses |w∂L/∂S| that depends on the wage rate. But there is also the value of propensity to seek healthcare ∂L/∂S. And this value represents a real pitfall for insurance companies.
Facing the problem of moral hazard, insurers are dreaming about “ideal customer” who has no spare time to visit doctors. Other words, they are looking for people with high marginal value of time. The model of the optimal consumption-leisure choice equitizes the marginal value of time with marginal costs of search (Malakhov 2015). And the latter depends not only on income but also on the propensity to search. The inequality of marginal values of the healthcare seeking (Equation 6) can be formed not only by high values of income w and unfair premiums wLC=QPC, but also by an important investment in ex ante healthcare Sex ante. People who really take care of their health do not stop after the purchase of the insurance policy. They continue to seek healthcare, now with means of insurance. And they substitute leisure H for healthcare seeking Sex post. They are really healthcare seekers. Unfortunately, health economics paid little attention to that phenomenon but sometimes it discovers interesting trends. For example, Ç.Koç (2005) stated the fact that the econometric results indicated that the moral hazard effect for physician visit was higher at relatively higher levels of wealth.
Does it mean that the behavior of healthcare seekers can turn to moral hazard even when the insurance policy is fair? Other words, does a fair insurance contract cannot eliminate moral hazard? Theoretically, the answer for these questions is negative because the fair insurance policy equalizes total marginal efforts, labor and healthcare seeking, with the marginal benefit on purchase. The consumer finds an option that satisfices him. The “it’s enough” reasoning stops immediately any additional effort. This additional effort, here again we come to our simple mathematics, rises the marginal benefit faster than marginal losses. And the consumer gets another, inverse inequality of marginal values. This new inequality corresponds to the steeper utility level, which stays below the moral hazard utility UMH (Fig.7):
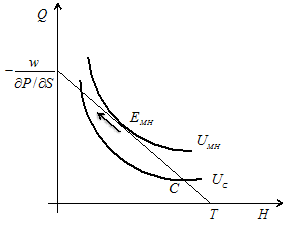
Figure 7. Stability of moral hazard solution.
The same effect takes place when an applicant receives a fair offer. Having such an offer, the customer does not need any moral hazard effort because it decreases his utility. Even when the consumer starts smoking after the purchase of full coverage, he understands that now he should loose some time on the chest X-ray.
Here we can also get the answer to the question what happens if a customer with zero precautionary efforts buys the full coverage at the equilibrium price level and then changes his behavior that results in moral hazard. The previous analysis of the equilibrium price dispersion discovers the trend when “shoppers”, people with zero search costs, become “searchers” with positive search costs (Malakhov 2016). There producers are willing to create a new market and they add to their product some complementary services. If “shoppers” accept new high prices, they pay. But if reasons for a new price seem to be unfair, “shoppers” become “searchers” and they begin to look for a lower price. The same effect takes place in insurance. If the price for full coverage looks unfair for an applicant who does not make any precautionary effort, it means that the absolute value of the marginal propensity to seek healthcare, here with zero precautionary effort but with high willingness to pay, is greater than the marginal benefit and total costs on insurance are greater that equilibrium expenditures (Eq.10):
![]()
Substituting some leisure time H by healthcare seeking time Sex post, the “shopper” becomes a “searcher”. He adds to his labor time some healthcare seeking time and begins to visit physicians (Fig.8):
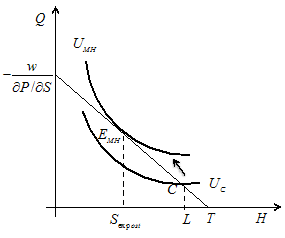
Figure 8. Moral hazard of individual with zero ax ante healthcare seeking costs.
There is another interesting question. Does the equilibrium under moral hazard EMC represents a real optimal solution? The reaction of insurance companies on moral hazard effect tells us that the answer for that question is also negative. But it means that our analysis is not finished yet and we should try to find a solution, which would be optimal not only for consumers but also for insurance companies.
4. Moral Hazard and the Competitive Equilibrium
For the moment, the moral hazard solution does not look as the competitive equilibrium but like some derivative of a monopoly offer. To find the competitive solution we should come back to the equilibrium price dispersion where offers of insurance companies depends on different propensities to seek healthcare and where they are ready to increase time horizons of insurance policies for careful applicants.
If we come back to the inequality of marginal values of health care seeking (Equation 6), we can see that the great absolute value of marginal costs can be diminished by the increase in the time horizon T of the consumption-leisure choice, i.e., by the prolongation of the insurance policy. The implementation of consumer-driving health plans (CDHP) demonstrates that it is possible. Employers create for their employees special accounts that can be carried over indefinitely into retirement by individuals with low health care expenditures (Farnsworth 2006, p.265). And we can see that the increase in the time horizon provides an individual with more leisure at the same level of consumption, which becomes optimal Q* under new terms (Fig.9):

Figure 9.Competitive equilibrium under new time horizon.
Here an individual can increase his utility not only with respect to the initial offer, that is obvious with the same level of consumption and with the increase in leisure time, but also with respect to possible moral hazard solution. If an individual gets an unfair offer, i.e., unfair price, he could plan in advance some moral hazard efforts in order to compensate the unfair price. The increase in time horizon discovers this hidden action and the new contract proposes a trade-off between price wL=QP and time horizon T. And moral hazard becomes uninteresting as well as inefficient.
5. Conclusion
The theory of the optimal-consumption leisure choice under price dispersion describes the phenomenon of moral hazard as the customer’s reaction on unfair insurance policy. The unfair insurance offer does not equalize marginal costs of propensity to seek healthcare with marginal benefits on purchase. Under unfair insurance policy consumers increase ex post healthcare seeking activities and they optimize their consumption of medical services. The analysis of moral hazard results in the assumption that the increase in the time horizon of the unfair insurance policy makes it fair and moral hazard becomes inefficient. The time horizon competition between insurance companies can eliminate moral hazard effect that clears the way to the competitive equilibrium.
References
- Aguiar, M. and Hurst, E., 2007. Measuring Trends in Leisure: The Allocation of Time Over Five Decades. Quarterly Journal of Economics, 122 (3), pp.969-1006.
- Arrow, K.J., 1963. Uncertainty and the Welfare Economics of Medical Care. American Economic Review, 53, pp.941-973.
- Ben-Shahar,O., Logue, K.D., 2012. Outsourcing Regulation: How Insurance Reduces Moral Hazard. 111 Michigan Law Review 197, pp.198-248.
- Doherty, N.A., O'Dea, B.A., Singer, H.J., 2004. The Secondary Market For Life Insurance Policies: Uncovering Life Insurance's "Hidden" Value. Marquette Elder's Advisor, 6 (1), pp.95-124.
- Farnsworth, D., 2006. Moral Hazard in Health Insurance: are consumer-directed plans the answer?. Annals health law, 15 (2), pp.251-273.
- Gladwell, M., 2005. The Myth of Moral Hazard. The New Yorker, August 25.
- Jerome, K.J., 1889. Three men in a boat (to say nothing of the dog). Bristol: J.W.Arrowsmith. London: Simpkin, Marshall, Hamilton, Kent & Co., Limited.
- Malakhov, S., 2014. Satisficing Decision Procedure and Optimal Consumption-Leisure Choice. International Journal of Social Science Research, 2 (2), pp.138-151. doi:10.5296/ijssr.v2i2.6158
- Malakhov, S., 2015) 'Propensity to Search: Common, Leisure, and Labor Models of Consumer Behavior' Expert Journal of Economics, 3 (1), pp.63-76.
- Malakhov, S., 2016) 'Law of One Price and Optimal Consumption-Leisure Choice Under Price Dispersion' Expert Journal of Economics, 4 (1), pp.1-8.
- Keenan, M., Seltzer, S., 2006. Life Settlements: investors beware. Journal of Payment Systems Law, 2 (7), pp.670-674.
- Koç, Ç., 2005. Health-Specific Moral Hazard Effects. Southern Economic Journal, 72(1), pp.98-118.
- Stiglitz, J., 1983. Risk, Incentives and Insurance: the pure theory of moral hazard,. Geneva Papers on Risk and Insurance, 8(1), pp.4-33.
- Zwietfel, P., Manning, W.G., 2000. Moral Hazard and Consumer Incentives in Health Care. Handbook of Health Economics, 1, pp.409-459.
- Zwietfel, P., Breyer, F., Kifmann, M., 2009. Health Economics. Springer-Verlag Berlin Heidelberg.
Article Rights and License
© 2017 The Author. Published by Sprint Investify. ISSN 2359-7712. This article is licensed under a Creative Commons Attribution 4.0 International License.


